Soal dan Pembahasan | Relasi Dan Fungsi

Soal-soal dan pembahasan materi  relasi dan fungsi untuk matematika SMP, dipilih dari soal-soal yang sebelumnya sudah  diujikan pada kegiatan  Ujian Sekolah, soal Ujian Nasional, dan soal lainnya.

RELASI DUA HIMPUNAN

---

Relasi dari himpunan $A$ ke himpunan $B$ adalah hubungan yang memasangkan anggota himpunan $A$ dengan anggota himpunan $B$.

Misal himpunan $A=\left\{ 1,2,4 \right\}$ dan himpunan $B=\left\{ (1,1),(1,2),(1,4),(2,2),(2,4),(4,4) \right\}$ mempunyai relasi bahwa himpunan $A$ merupakan faktor dari himpunan $B$. Relasi himpunan $A$ dan himpunan $B$ dapat dinyatakan dalam tiga cara yaitu:

• Diagram panah

• 
  
  
  

  
  
  
  

  
  

  
  
  

  
  

• Koordinat Kartesius

• 
  
  
  
  
  

  
  
  

  
  

• Himpunan pasangan terurut

• $\left\{ (1,2),(1,3),(1,4),(2,2),(2,4),(4,4) \right\}$

---

FUNGSI (PEMETAAN)

---

Fungsi (pemetaan) dari himpunan $A$ ke himpunan $B$ adalah hubungan yang memasangkan tepat satu anggota himpunan $A$ dengan anggota himpunan $B$.

Jika himpunan $A$ adalah Domain (daerah asal) dan himpunan $B$ adalah kodomain (daerah kawan) maka relasi himpunan $A$ ke himpunan $B$ merupakan fungsi saat anggota domain mempunyai pasangan tepat satu pada kodomain.

Relasi himpunan $A$ ke himpunan $B$ di atas adalah contoh relasi yang merupakan fungsi karena anggota pada domain (daerah asal) $A$ mempunyai pasangan tepat satu di kodomain (daerah kawan) $B$, yaitu $\left\{ (a,y),(b,z),(c,z) \right\}$.
Pada diagram panah di atas kita peroleh Range (daerah hasil) yaitu $\left\{ y,z \right\}$

Relasi himpunan $A$ ke himpunan $B$ di atas adalah contoh relasi yang bukan fungsi karena anggota pada domain $A$ ada yang mempunyai pasangan di kodomain $B$ lebih dari satu, yaitu $\left\{ (b,x) \right\}$ dan $\left\{ (b,z) \right\}$.

Jika himpunan $A$ banyak anggota adalah $n(A)$ dan himpunan $B$ banyak anggota adalah $n(B)$, maka banyaknya fungsi (pemetaan) yang dapat terjadi dapat kita hitung dengan rumus:
\begin{align}
n \left(A \longrightarrow B \right)\ & = n(B)^{n(A)} \\ n \left(B \longrightarrow A \right)\ & = n(A)^{n(B)} \end{align}

---

NOTASI FUNGSI dan NILAI FUNGSI

---

Notasi fungsi umumnya ditulis dalam bentuk $f : x \longrightarrow y$ atau $f : x \longrightarrow f(x)$ menjadi $f(x)=y$, dibaca "fungsi $f$ memetakan $x$ ke $y$". $f(x)$ merupakan hasil peta bayangan dari $x$.

Untuk nilai fungsi dari suatu domain, hasil yang diperoleh disebut juga daerah hasil (range).
Misalnya diketahui fungsi $f(x)=2x+3$, maka nilai fungsi untuk $x=1$ dinyatakan dalam bentuk:
$\begin{align}
f(x) & = 2x+3 \\
f(1) & = 2(1)+3 \\
& = 2+3 \\
& = 5 \end{align}$

SOAL LATIHAN dan PEMBAHASAN - Relasi dan Fungsi

1. Soal UNBK Matematika SMP 2019

Perhatikan diagram panah berikut!

Rumus fungsi dari $A$ ke $B$ adalah...

$\begin{align}

(A)\ & f(x)=-3x-2 \\

(B)\ & f(x)=x+2 \\

(C)\ & f(x)=2x+3 \\

(D)\ & f(x)=3x+4

\end{align}$

Alternatif Pembahasan:

Pilihan pada fungsi adalah fungsi linear, sehingga fungsi dapat kita
misalkan dengan $f(x)=ax+b$

$\begin{align}

f(-1) &: -a+b=1 \\

f(0) &: b=3 \\

f( 1) &: a+b=5 \\

\hline

a & = 2 \\

f(x) &= 2x+3

\end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ f(x)=2x+3$

2. Soal Simulasi UNBK Matematika SMP 2019

Diagram panah di samping menunjukkan fungsi dari $x$ ke $f(x)$. Tumus
fungsinya adalah...

Rumus fungsi dari $A$ ke $B$ adalah...

$\begin{align}

(A)\ & f(x)=x+10 \\

(B)\ & f(x)=2x+4 \\

(C)\ & f(x)=4x-2 \\

(D)\ & f(x)=6x-5

\end{align}$

Alternatif Pembahasan:

Dari gambar diagram panah,

Untuk $x=3$ diperoleh $f(3)=13$

Untuk $x=5$ diperoleh $f(5)=25$

Untuk $x=6$ diperoleh $f(6)=31$



Kita misalkan $f(x)=mx+n$ sehingga kita peroleh:

$f(3)=3m+n\ \Rightarrow 3m+n=13$

$f(5)=5m+n\ \Rightarrow 5m+n=25$

$f(6)=6m+n\ \Rightarrow 6m+n=31$



Dengan mengeliminasi atau substitusi;

$\begin{array}{c|c|cc}

3m+n = 13 & \\

5m+n = 25 & - \\

\hline

-2m = -12 \\

m = 6 \\

n = -5 \\

f(x)=6x-5

\end{array} $



$\therefore$ Pilihan yang sesuai adalah $(D)\ f(x)=6x-5$

3. Soal UNBK Matematika SMP 2018

Perhatikan diagram panah berikut!

Rumus fungsi dari $A$ ke $B$ adalah....

$\begin{align}

(A)\ & f(x)=2x+3 \\

(B)\ & f(x)=5x-12 \\

(C)\ & f(x)=3x-2 \\

(D)\ & f(x)=2x-3

\end{align}$

Alternatif Pembahasan:

Dari gambar diagram panah,

Nilai $a_{1}=5$ menjadi $b_{1}=13$

Nilai $a_{2}=6$ menjadi $b_{2}=15$

Nilai $a_{3}=8$ menjadi $b_{3}=19$

Perubahan nilai dari $A$ ke $B$ yang paling cocok adalah $f(x)=2x+3$.

$f(5)=2(5)+3=13$

$f(6)=2(6)+3=15$

$f(8)=2(8)+3=19$



$\therefore$ Pilihan yang sesuai adalah $(A)\ f(x)=2x+3$

4. Soal UNBK Matematika SMP 2018 

Diketahui rumus fungsi $f(x) = 5x – 2$. Jika $f(m) = 18$ dan $f(n) = 23$.
Nilai $m + n$ adalah...

$\begin{align}

(A)\ & 4 \\

(B)\ & 8 \\

(C)\ & 9 \\

(D)\ & 12

\end{align}$

Alternatif Pembahasan:

Dari apa yang diketahui pada soal, jika kita substitusi nilai $f(m) = 18$
dan $f(n) = 23$ ke $f(x) = 5x – 2$, kita akan peroleh;


$\begin{align}

f(x) &=5x-2 \\

f(m)\ &=5m-2 \\

18\ &=5m-2 \\ 18+2\ &=5m \\ 20\ &=5m \longrightarrow
m=\dfrac{20}{5}=4 \\ \hline f(n)\ &=5(n)-2 \\

23\ &=5n-2 \\ 23+2\ &=5n \\ 25\ &=5n \longrightarrow
n=\dfrac{25}{5}=5 \\ \end{align}$

Nilai $m + n=4+5=9$.

$\therefore$ Pilihan yang sesuai adalah $(C)\ 9$

5. Soal Simulasi UNBK Matematika SMP 2018

Diketahui fungsi $f(x)=-2x+3$. Nilai dari $f(a+5)$ adalah...

$\begin{align}

(A)\ & 2a+13 \\ (B)\ & 2a-7 \\ (C)\ & -2a-13 \\ (D)\ & -2a-7


\end{align}$

Alternatif Pembahasan:

Fungsi $f(x)=-2x+3$ adalah sebuah fungsi dengan variabel $(\text{peubah})\
x$, fungsi bisa kita rubah sesuai dengan variabel yang kita inginkan,
misal:

$\begin{align} f(x) &= -2x+3 \\ f(m) &= -2m+3 \\ f(k) &= -2k+3
\\ f(abc) &= -2abc+3 \\ f(💗) &= -2💗+3 \end{align}$

dan sebagainya.

Dengan memahami perubahan variabel fungsi diatas, mainear ka kita sudah bisa
merubah variabel $x$ menjadi $a+5$.

$\begin{align} f(x) &= -2x+3 \\ f(a+5) &=-2(a+5)+3 \\ &=-2a-10+3
\\ &=-2a-7 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ -2a-7$

6. Soal Fungsi

Daerah hasil untuk $f(x)=2x+1$ $x \in \text{Bilangan Cacah}$ adalah...

$\begin{align}

(A)\ & \text{Bilangan bulat} \\ (B)\ & \text{Bilangan ganjil} \\ (C)\
& \text{Bilangan asli} \\ (D)\ & \text{Bilangan real} \end{align}$

Alternatif Pembahasan:

Untuk $x \in \text{Bilangan Cacah}$ maka nilai $f(x)=2x+1$ dapat kita
simpulkan:

$\begin{align}

f(0) & =2(0)+1=1\\ f(1) & =2(1)+1=3\\ f(2) & =2(2)+1=5\\ f(3)
& =2(3)+1=7 \vdots

\end{align}$

Semua pilihan jawaban pada soal benar, tetapi karena diharuskan memilih maka
pilihan kita ada pada $(B)\ \text{Bilangan ganjil}$.



$\therefore$ Pilihan yang sesuai adalah $(C)\ \text{Bilangan ganjil}$

7. Soal Relasi

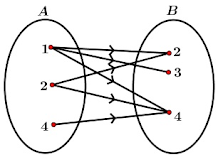
Perhatikan diagram berikut!

Relasi dari himpunan $A$ ke himpunan $B$ adalah...

$\begin{align} (A)\ & \text{lebih dari} \\ (B)\ & \text{kurang dari}
\\ (C)\ & \text{setengah dari} \\ (D)\ & \text{faktor dari}
\end{align}$

Alternatif Pembahasan:

• Anggota $(A)$ yaitu $1$ berelasi ke $(B)$ pada $2,\ 3,\ 4$


• Anggota $(A)$ yaitu $2$ berelasi ke $(B)$ pada $2,\ 4$


• Anggota $(A)$ yaitu $4$ berelasi ke $(B)$ pada $4$

Dari data di atas relasi yang bisa mewakili semua relasi adalah "Faktor Dari"

$\therefore$ Pilihan yang sesuai adalah $(D)\ \text{faktor dari}$

8. Soal Fungsi

Diagram panah dibawah ini yang merupakan pemetaan adalah...

Alternatif Pembahasan:

Pemetaan atau fungsi adalah relasi himpunan dimana semua anggota daerah asal
(domain) mempunyai pasangan tepat satu pada daerah kawan (kodomain).

Gambar diagram panah yang memenuhi syarat pemetaan atau fungsi adalah
diagram panah pilihan $(D)$



$\therefore$ Pilihan yang sesuai adalah $(D)$

9. Soal Fungsi

Jika $f(x-1)=2x+3$ maka $f(2)=\cdots$

$\begin{align}

(A)\ & 8 \\ (B)\ & 9 \\ (C)\ & 10 \\ (D)\ & 11

\end{align}$

Alternatif Pembahasan:

Dari fungsi $f(x-1)=2x+3$, yang ditanyakan adalah $f(2)$ maka kita
substitusi $x=3$ agar pada $f(x-1)$ kita peroleh $f(2)$.

$\begin{align}

f(x-1) & = 2x+3 \\ f(3-1) & = 2(3)+3 \\ f(2) & = 6+3 \\ f(2)
& = 9

\end{align}$



$\therefore$ Pilihan yang sesuai adalah $(B)\ 9$

10. Soal UN Matematika SMP 2018 

Perhatikan diagram panah berikut!

Rumus fungsi dari $P$ ke $Q$ adalah...

$\begin{align}

(A)\ & f(x)=4 \left( 2x+5 \right) \\

(B)\ & f(x)=3 \left( 2x+3 \right) \\

(C)\ & f(x)=2 \left( 3x+9 \right) \\

(D)\ & f(x)=\dfrac{1}{2} \left( 6x+18 \right)

\end{align}$

Alternatif Pembahasan:

Pilihan pada fungsi adalah fungsi linear, sehingga fungsi dapat kita
misalkan dengan $f(x)=ax+b$

$\begin{align}

f(2)=21 & \longrightarrow 2a+b=21\ \text{(pers.1)} \\ f(6)=45 &
\longrightarrow 6a+b=45\ \text{(pers.2)} \\ f(10)=69 & \longrightarrow
10a+b=69\ \text{(pers.3)} \end{align}$

Dari persamaan $\text{pers.1}$ dan $\text{pers.2}$ kita peroleh:

$\begin{align}

2a+b &=21 \\ 6a+b &=45\ \ (-) \\ \hline 4a &=24\ \longrightarrow
a=\dfrac{24}{4}=6 \\ 2a+b &=21 \\ 2(6)+b &=21 \\ 12+b &=21\
\longrightarrow b=9 \\ \end{align}$

Untuk $a=6$ dan $b=9$ maka $f(x)=6x+9=3 \left( 2x+3 \right)$

$\therefore$ Pilihan yang sesuai adalah $(C)\ f(x)=3 \left( 2x+3 \right)$

11. Soal UN Matematika SMP 2018 

Diketahui rumus fungsi $f(x) = 2x – 3$. Jika $f(m) = 5$ dan $f(-2) = n$. Nilai
$m + n$ adalah...

$\begin{align}

(A)\ & 5 \\

(B)\ & 2 \\

(C)\ & -3 \\

(D)\ & -6

\end{align}$

Alternatif Pembahasan:

Dari apa yang diketahui pada soal, jika kita substitusi nilai $f(m) = 5$ dan
$f(-2) = n$ ke $f(x) = 2x – 3$, kita akan peroleh;


$\begin{align}

f(x) &=2x-3 \\

f(m)\ &=2m-3 \\

5\ &=2m-3 \\ 5+3\ &=2m \\ 8\ &=2m \longrightarrow
m=\dfrac{8}{2}=4 \\ \hline f(-2)\ &=2(-2)-3 \\

n\ &=-4-3 \\ n\ &=-7 \end{align}$

Nilai $m + n=4-7=-3$.

$\therefore$ Pilihan yang sesuai adalah $(C)\ -3$

12. Soal UN Matematika SMP 2018

Perhatikan gambar di samping!

Relasi yang tepat dari himpunan $A$ ke himpunan $B$ adalah...

$\begin{align} (A)\ & \text{kuadrat dari} \\ (B)\ & \text{kurang dari}
\\ (C)\ & \text{faktor dari} \\ (D)\ & \text{lebih dari} \end{align}$

Alternatif Pembahasan:

• Anggota $(A)$ yaitu $2$ berelasi ke $(B)$ pada $2,\ 4,\ 6,\ 8$


• Anggota $(A)$ yaitu $3$ berelasi ke $(B)$ pada $6$


• Anggota $(A)$ yaitu $4$ berelasi ke $(B)$ pada $4,\ 8$

Dari data di atas relasi yang bisa mewakili semua relasi adalah "Faktor Dari"

$\therefore$ Pilihan yang sesuai adalah $(C)\ \text{faktor dari}$

13. Soal UN Matematika SMP 2017

Diketahui rumus fungsi $f(x) = 2x – 5$. Jika $f(k) = -15$ maka nilai $k$
adalah...

$\begin{align}

(A)\ & -10 \\

(B)\ & -5 \\

(C)\ & 5 \\

(D)\ & 10

\end{align}$

Alternatif Pembahasan:

Dari apa yang diketahui pada soal, jika kita substitusi nilai $f(k) = -15$
ke $f(x) = 2x – 5$, kita akan peroleh;


$\begin{align}

f(x) &=2x-5 \\

f(k)\ &=2k-5 \\

-15\ &=2k-5 \\ -15+5\ &=2k \\ -10\ &=2k \longrightarrow
k=\dfrac{-10}{2}=-5 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ -5$

14. Soal UN Matematika SMP 2016

Diketahui $A= \{ a,b,c \}$ dan $B= \{ 1,2,3,4,5 \}$. Banyak pemetaan yang
mungkin dari $A$ ke $B$ adalah...

$\begin{align} (A)\ & 15 \\ (B)\ & 32 \\ (C)\ & 125 \\ (D)\ &
243 \end{align}$

Alternatif Pembahasan:

Jika himpunan $A$ banyak anggota adalah $n(A)$ dan himpunan $B$ banyak
anggota adalah $n(B)$, maka banyaknya fungsi (pemetaan) yang dapat terjadi
dapat kita hitung dengan rumus:

\begin{align}

n \left(A \longrightarrow B \right)\ & = n(B)^{n(A)} \end{align}

Untuk $A= \{ a,b,c \}$ maka $n(A)=3$ dan $B= \{ 1,2,3,4,5 \}$, $n(B)=5$ maka
banyak pemetaan yang mungkin dari $A$ ke $B$ adalah $n(B)^{n(A)}=5^{3}=125$.

$\therefore$ Pilihan yang sesuai adalah $(C)\ 125$

15. Soal UN Matematika SMP 2016

Fungsi $f$ dinyatakan dengan $f(x) = 3x+5 $. Hasil dari $f \left(2b-3 \right)$
adalah...

$\begin{align}

(A)\ & 5b+8 \\

(B)\ & 5b+2 \\

(C)\ & 6b-4 \\

(D)\ & 6b-15 \end{align}$

Alternatif Pembahasan:

Dari apa yang diketahui pada soal, jika kita substitusi nilai $f \left(2b-3
\right)$ ke $f(x) = 3x+5 $, kita akan peroleh;


$\begin{align}

f(x) &=3x+5 \\

f(2b-3)\ &=3(2b-3)+5 \\

&=6b-9+5 \\ &=6b-4 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(C)\ 6b-4$

16. Soal UN Matematika SMP 2015

Diketahui rumus fungsi $f(x) = 3x+2 $. Nilai dari $f \left( 4y-7 \right)$
adalah...

$\begin{align}

(A)\ & 12y-23 \\

(B)\ & 12y-19 \\

(C)\ & 12y-11 \\

(D)\ & 12y-5 \end{align}$

Alternatif Pembahasan:

Dari apa yang diketahui pada soal, jika kita substitusi nilai $f \left( 4y-7
\right)$ ke $f(x) = 3x+2 $, kita akan peroleh;


$\begin{align}

f(x) &=3x+2 \\

f(4y-7)\ &=3( 4y-7)+2 \\

&=12y-21+2 \\ &=12y-19 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ 12y-19$

17. Soal UN Matematika SMP 2015

Perhatikan himpunan pasangan berikut:

1. $\{ (1,a),(2,b),(3,b) \}$


2. $\{ (1,a),(1,b),(3,c) \}$


3. $\{ (2,4),(4,8),(6,12) \}$


4. $\{ (2,4),(2,8),(6,12) \}$

Himpunan pasangan yang merupakan pemetaan adalah...

$\begin{align}

(A)\ & 1\ \text{dan}\ 2 \\ (B)\ & 1\ \text{dan}\ 3 \\ (C)\ & 2\
\text{dan}\ 3 \\ (D)\ & 1\ \text{dan}\ 2 \end{align}$

Alternatif Pembahasan:

Fungsi (pemetaan) dari himpunan $A$ ke himpunan $B$ adalah hubungan yang
memasangkan tepat satu anggota himpunan $A$ dengan anggota himpunan $B$.

Dari himpunan pasangan di atas yang merupakan pemetaan adalah $1\
\text{dan}\ 3$.

1. $\{ (1,a),(2,b),(3,b) \}$ adalah Fungsi (pemetaan)


2. 
   $\{ (1,a),(1,b),(3,c) \}$ tidak Fungsi (pemetaan) karena $1$ mempunyai dua
   pasangan di kodomain yaitu $a$ dan $b$
   


3. $\{ (2,4),(4,8),(6,12) \}$ adalah Fungsi (pemetaan)


4. 
   $\{ (2,4),(2,8),(6,12) \}$ tidak Fungsi (pemetaan) karena $2$ mempunyai
   dua pasangan di kodomain yaitu $4$ dan $8$
   

$\therefore$ Pilihan yang sesuai adalah $(B)\ 1\ \text{dan}\ 3$

18. Soal UN Matematika SMP 2018

Suatu perusahaan taksi memasang tarif seperti grafik berikut:

Alia pergi kerumah nenek yang berjarak $22$ kilometer dengan menggunakan taksi
tersebut. Berapa tarif taksi harus dibayar Alia?

$\begin{align} (A)\ & Rp66.000,00 \\ (B)\ & Rp73.000,00 \\ (C)\ &
Rp132.000,00 \\ (D)\ & Rp143.000,00 \end{align}$

Alternatif Pembahasan:

Dari gambar grafik tarif berupa garis lurus dapat kita peroleh sebagai
berikut:

Tarif Taksi
Jarak	Harga	Pola
$2$	$13$	$3(2)+7$
$4$	$19$	$3(4)+7$
$6$	$25$	$3(6)+7$
$\vdots$	$\vdots$	$\vdots$
$22$	$\cdots$	$3(22)+7=73$

$\therefore$ Pilihan yang sesuai adalah $(B)\ Rp73.000,00$

19. Soal UN Matematika SMP 2018 

Fungsi $f(x) = 3x+9$. Jika $f(k) = 33$ maka nilai $k$ adalah...

$\begin{align}

(A)\ & 22 \\

(B)\ & 14 \\

(C)\ & 12 \\

(D)\ & 8

\end{align}$

Alternatif Pembahasan:

Dari apa yang diketahui pada soal, jika kita substitusi nilai $f(k) = 33$ ke
$f(x) = 3x+9$, kita akan peroleh;


$\begin{align}

f(x) &=3x+9 \\

f(k)\ &=3k+9 \\

33\ &=3k+9 \\ 33-9\ &=3k \\ 24\ &=3k \longrightarrow
k=\dfrac{24}{3}=8 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(D)\ 8$

20. Soal UN Matematika SMP 2012

Diketahui rumus fungsi $f(x) = -2x+5$. Nilai $f(-4)$ adalah...

$\begin{align}

(A)\ & -13 \\

(B)\ & -3 \\

(C)\ & 3 \\

(D)\ & 13

\end{align}$

Alternatif Pembahasan:

Dari apa yang diketahui pada soal, jika kita substitusi nilai $f(-4)$ ke
$f(x) = -2x+5$, kita akan peroleh;


$\begin{align}

f(x) &=-2x+5 \\

f(-4)\ &=-2(-4)+5\\

&=-8+5 \\ &=-3 \end{align}$

$\therefore$ Pilihan yang sesuai adalah $(B)\ -3$