Bangun Ruang (Pra-Olimpiade) Soal dan Pembahasan
Bangun ruang adalah suatu benda tiga dimensi yang memiliki ukuran panjang, lebar, dan tinggi. Di matematika, kita mengenal beberapa jenis bangun ruang seperti kubus, balok, prisma, limas, tabung, kerucut, dan bola. Berikut adalah penjelasan singkat tentang setiap jenis bangun ruang:
Kubus: Kubus adalah bangun ruang yang memiliki 6 sisi yang sama besar,
dan masing-masing sisi berbentuk persegi. Kubus juga memiliki 12 rusuk dan 8
sudut siku-siku.
Balok: Balok adalah bangun ruang yang memiliki 6 sisi, di mana 3 sisi
berbentuk persegi dan 3 sisi lainnya berbentuk persegi panjang. Balok juga
memiliki 12 rusuk dan 8 sudut.
Prisma: Prisma adalah bangun ruang yang memiliki 2 sisi datar dan
masing-masing sisi memiliki bentuk yang sama dan sejajar. Prisma juga memiliki
3 sisi lainnya yang berbentuk persegi atau segitiga dan 2 bidang alas yang
berbentuk segi-n.
Limas: Limas adalah bangun ruang yang memiliki alas berbentuk segitiga
atau segi-n, dan sisi-sisi miring yang bertemu pada sebuah titik. Limas juga
memiliki satu sisi datar yang berbentuk segitiga atau segi-n.
Tabung: Tabung adalah bangun ruang yang terdiri dari dua lingkaran
dengan jari-jari sama dan terhubung oleh sebuah silinder. Tabung juga memiliki
dua bidang alas yang berbentuk lingkaran dan satu sisi datar yang berbentuk
persegi atau persegi panjang.
Kerucut: Kerucut adalah bangun ruang yang terdiri dari sebuah lingkaran
dan sebuah sisi miring yang bertemu pada sebuah titik. Kerucut juga memiliki
sebuah bidang alas yang berbentuk lingkaran.
Bola: Bola adalah bangun ruang yang terdiri dari semua titik yang
berjarak sama dari sebuah titik tertentu yang disebut pusat bola. Bola juga
tidak memiliki rusuk dan sudut.
Dalam matematika, kita dapat menghitung luas permukaan dan volume dari setiap
jenis bangun ruang tersebut. Hal ini penting untuk mengetahui sifat-sifat dan
karakteristik dari setiap jenis bangun ruang serta aplikasinya dalam kehidupan
sehari-hari.
Berikut ini merupakan soal dan pembahasan mengenai bangun ruang yang dapat
dijadikan bahan untuk persiapan kompetisi dan olimpiade matematika. Alangkah
baiknya apabila soal dasar tentang bangun ruang dipelajari terlebih dahulu
agar lebih mudah memahami soal-soal yang ada pada postingan ini.
Tabel rumus berikut akan sangat berguna untuk mengerjakan soal-soal tentang bangun ruang.
$$\renewcommand{\arraystretch}{2} \begin{array}{|c|c|c|} \hline
\text{Bangun Ruang} & \text{Luas Permukaan} & \text{Luas Selimut}
& \text{Volume} \\ \hline \text{Kubus} & 6s^2 & 4s^2 & s^3
\\ \text{Balok} & 2(p \ell + pt + \ell t) & 2(pt + lt) & p \ell
t \\ \text{Limas segi-n} & L_A + L_{ST} & L_{ST} & \dfrac13
\cdot L_A \cdot t \\ \text{Prisma segi-n} & 2L_A + L_{ST} & L_{ST}
& L_A \cdot t \\ \text{Tabung} & 2\pi r(r + t) & 2\pi r t &
\pi r^2 t \\ \text{Kerucut} & \pi r(r + s) & \pi r s & \dfrac13
\pi r^2 t \\ \text{Bola (Pejal/Hampa)} & 4\pi r^2 & 4 \pi r^2 &
\dfrac43 \pi r^3 \\ \text{Setengah Bola (Pejal)} & 3\pi r^2 & 3 \pi
r^2 & \dfrac23 \pi r^3 \\ \text{Setengah Bola (Hampa)} & 2\pi r^2
& 2\pi r^2 & \dfrac23 \pi r^3\\ \hline \end{array}$$
Soal Nomor 1
Diketahui volume sebuah kubus adalah $2.744~\text{cm}^3$. Luas permukaan kubus tersebut adalah $\cdots \cdot$
A. $192~\text{cm}^2$
B. $384~\text{cm}^2$
C. $1.176~\text{cm}^2$
D. $2.352~\text{cm}^2$
E. $2.744~\text{cm}^2$
Pembahasan :
Diketahui $V = 2.744~\text{cm}^3.$ Misalkan $s$ adalah panjang rusuk kubus. Akan dicari nilai dari $L = 6s^2$.
$$\begin{aligned} V & = 2.744 \\ s^3 & = 2.744 \\ s & =
\sqrt[3]{2.744} = 14 \\ s^2 & = 14^2 = 196 \\ 6s^2 & = 6 \cdot
196 = 1.176~\text{cm}^2 \end{aligned}$$Jadi, luas permukaan kubus tersebut adalah $\boxed{1.176~\text{cm}^2}$
(Jawaban C)
Soal Nomor 2
Jika luas sisi depan, sisi samping, dan sisi bawah sebuah balok
masing-masing $x, y$, dan $z$, maka volume balok tersebut adalah $\cdots\cdot$
A. $x+y+z$
B. $xy+xz+yz$
C. $(xyz)^2$
D. $xyz$
E. $\sqrt{xyz}$
\text{Bangun Ruang} & \text{Luas Permukaan} & \text{Luas Selimut}
& \text{Volume} \\ \hline \text{Kubus} & 6s^2 & 4s^2 & s^3
\\ \text{Balok} & 2(p \ell + pt + \ell t) & 2(pt + lt) & p \ell
t \\ \text{Limas segi-n} & L_A + L_{ST} & L_{ST} & \dfrac13
\cdot L_A \cdot t \\ \text{Prisma segi-n} & 2L_A + L_{ST} & L_{ST}
& L_A \cdot t \\ \text{Tabung} & 2\pi r(r + t) & 2\pi r t &
\pi r^2 t \\ \text{Kerucut} & \pi r(r + s) & \pi r s & \dfrac13
\pi r^2 t \\ \text{Bola (Pejal/Hampa)} & 4\pi r^2 & 4 \pi r^2 &
\dfrac43 \pi r^3 \\ \text{Setengah Bola (Pejal)} & 3\pi r^2 & 3 \pi
r^2 & \dfrac23 \pi r^3 \\ \text{Setengah Bola (Hampa)} & 2\pi r^2
& 2\pi r^2 & \dfrac23 \pi r^3\\ \hline \end{array}$$
BAGIAN PILIHAN GANDA
Soal Nomor 1
Diketahui volume sebuah kubus adalah $2.744~\text{cm}^3$. Luas permukaan kubus tersebut adalah $\cdots \cdot$
A. $192~\text{cm}^2$
B. $384~\text{cm}^2$
C. $1.176~\text{cm}^2$
D. $2.352~\text{cm}^2$
E. $2.744~\text{cm}^2$
Pembahasan :
Diketahui $V = 2.744~\text{cm}^3.$ Misalkan $s$ adalah panjang rusuk kubus. Akan dicari nilai dari $L = 6s^2$.
$$\begin{aligned} V & = 2.744 \\ s^3 & = 2.744 \\ s & =
\sqrt[3]{2.744} = 14 \\ s^2 & = 14^2 = 196 \\ 6s^2 & = 6 \cdot
196 = 1.176~\text{cm}^2 \end{aligned}$$Jadi, luas permukaan kubus tersebut adalah $\boxed{1.176~\text{cm}^2}$
(Jawaban C)
Soal Nomor 2
Jika luas sisi depan, sisi samping, dan sisi bawah sebuah balok
masing-masing $x, y$, dan $z$, maka volume balok tersebut adalah $\cdots\cdot$
A. $x+y+z$
B. $xy+xz+yz$
C. $(xyz)^2$
D. $xyz$
E. $\sqrt{xyz}$
Pembahasan :
Misalkan panjang, lebar, dan tingginya dinyatakan oleh $p, \ell$, dan $t$ sehingga $V = p \ell t.$
Diketahui bahwa $pt= x$, $p \ell = y$, dan $\ell t = z$. Dengan mengkuadratkan volume, kita peroleh
$$\begin{aligned} V^2 & = (p \ell t)^2 \\ V^2 & = (pt)(p \ell)(\ell t) \\ V^2 & = xyz \\ V & = \sqrt{xyz} \end{aligned}$$Jadi, volume balok tersebut adalah $\boxed{\sqrt{xyz}}$
(Jawaban E)
Soal Nomor 3
Jika rasio panjang, lebar, dan tinggi sebuah balok adalah $1 : 3 : 5$
dan luas permukaan balok adalah $4.600~\text{cm}^2$, maka volumenya adalah $\cdots \cdot$
A. $1.500~\text{cm}^3$
B. $3.000~\text{cm}^3$
C. $9.000~\text{cm}^3$
D. $15.000~\text{cm}^3$
E. $30.000~\text{cm}^3$
Pembahasan :
Diketahui p : $\ell : t = 1 : 3 : 5$.
Dapat kita tulis $p = x$, $\ell = 3x$, dan $t = 5x$ untuk suatu bilangan asli $x$. Karena $L = 4.600~\text{cm}^2$, maka kita peroleh
$$\begin{aligned} 2(p \ell + pt + \ell t) & = 4.600 \\ x(3x) + x(5x) + 3x(5x) & = 2.300 \\ 3x^2 + 5x^2 + 15x^2 & = 2.300 \\ 23x^2 & = 2.300 \\ x^2 & = 100 \\ \Rightarrow x & = 10 \end{aligned}$$Ingat bahwa $x$ adalah bilangan asli sehingga $x \neq -10$.
Jadi, panjang, lebar, dan tinggi balok tersebut berturut-turut adalah $p = 10~\text{cm}$, $\ell = 30~\text{cm}$, dan $t = 50~\text{cm}$.
Selanjutnya, akan dicari volume balok.
$$\begin{aligned} V & = p \ell t \\ & = 10(30)(50) \\ & = 15.000~\text{cm}^3 \end{aligned}$$Jadi, volume balok tersebut adalah $\boxed{15.000~\text{cm}^3}$
(Jawaban D)
Soal Nomor 4
Jumlah panjang jari-jari alas dan tinggi suatu tabung adalah $37$ meter. Jika luas permukaan tabung itu adalah $1.628~\text{m}^2$ dan asumsikan $\pi = \dfrac{22}{7}$, maka volume tabung adalah ....
A. $660~\text{m}^3$
B. $2.310~\text{m}^3$
C. $4.620~\text{m}^3$
D. $9.240~\text{m}^3$
E. $32.340~\text{m}^3$
Pembahasan :
Diketahui $r + t = 37~\text{m}$ dan $L_p = 1.628~\text{m}^2.$
Pertama, akan dicari panjang jari-jari alas tabung.
$$\begin{aligned} L_p & = 1.628 \\ 2 \pi r(\color{blue}{r + t}) & = 1.628 \\ 2 \cdot \dfrac{22}{7} \cdot r(37) & = 1.628 \\ r & = \dfrac{1.628 \cdot 7}{2 \cdot 37 \cdot 22} \\ r & =
7~\text{m} \end{aligned}$$Karena $r + t = 37~\text{m}$ dan $r =7~\text{m}$, maka $t = 30~\text{m}$. Dengan demikian,
$$\begin{aligned} V & = \pi r^2 t \\ & = \dfrac{22}{7}\cdot 7^2 \cdot 30 \\ & = 4.620~\text{m}^3 \end{aligned}$$Jadi, volume tabung tersebut adalah $\boxed{4.620~\text{cm}^3}$
(Jawaban C)
Soal Nomor 5
Rasio luas permukaan dan luas selimut sebuah tabung yang alasnya berjari-jari $80~\text{cm}$ dan tingginya $20~\text{cm}$ adalah $\cdots\cdot$
A. $3 : 1$
B. $4 : 1$
C. $5 : 1$
D. $10 : 1$
E. $12 : 1$
Pembahasan :
Diketahui $r = 80~\text{cm}$ dan $t = 20~\text{cm}.$
Perbandingan (rasio) luas permukaan dan luas selimut tabung
dinyatakan sebagai berikut.
$$\begin{aligned} L_p : L_s & = \cancel{2\pi r}(r + t) :
\cancel{2\pi r} t \\ & = (r + t) : t \\ & = (80 + 20) : 20
\\ & = 100 : 20 \\ & = 5 : 1 \end{aligned}$$Jadi, rasio luas
permukaan dan luas selimut tabung tersebut adalah $\boxed{5 :1}$
(Jawaban C)
Soal Nomor 6
Dua buah tabung yang bervolume sama mempunyai tinggi dengan perbandingan $1 : 2$. Perbandingan panjang jari-jari kedua tabung tersebut adalah $\cdots \cdot$
A. $1 : \sqrt2$
B. $\sqrt2 : 1$
C. $1 : 2$
D. $2 : 1$
E. $2\sqrt2 : 1$
Misalkan panjang, lebar, dan tingginya dinyatakan oleh $p, \ell$, dan $t$ sehingga $V = p \ell t.$
Diketahui bahwa $pt= x$, $p \ell = y$, dan $\ell t = z$. Dengan mengkuadratkan volume, kita peroleh
$$\begin{aligned} V^2 & = (p \ell t)^2 \\ V^2 & = (pt)(p \ell)(\ell t) \\ V^2 & = xyz \\ V & = \sqrt{xyz} \end{aligned}$$Jadi, volume balok tersebut adalah $\boxed{\sqrt{xyz}}$
(Jawaban E)
Soal Nomor 3
Jika rasio panjang, lebar, dan tinggi sebuah balok adalah $1 : 3 : 5$
dan luas permukaan balok adalah $4.600~\text{cm}^2$, maka volumenya adalah $\cdots \cdot$
A. $1.500~\text{cm}^3$
B. $3.000~\text{cm}^3$
C. $9.000~\text{cm}^3$
D. $15.000~\text{cm}^3$
E. $30.000~\text{cm}^3$
Pembahasan :
Diketahui p : $\ell : t = 1 : 3 : 5$.
Dapat kita tulis $p = x$, $\ell = 3x$, dan $t = 5x$ untuk suatu bilangan asli $x$. Karena $L = 4.600~\text{cm}^2$, maka kita peroleh
$$\begin{aligned} 2(p \ell + pt + \ell t) & = 4.600 \\ x(3x) + x(5x) + 3x(5x) & = 2.300 \\ 3x^2 + 5x^2 + 15x^2 & = 2.300 \\ 23x^2 & = 2.300 \\ x^2 & = 100 \\ \Rightarrow x & = 10 \end{aligned}$$Ingat bahwa $x$ adalah bilangan asli sehingga $x \neq -10$.
Jadi, panjang, lebar, dan tinggi balok tersebut berturut-turut adalah $p = 10~\text{cm}$, $\ell = 30~\text{cm}$, dan $t = 50~\text{cm}$.
Selanjutnya, akan dicari volume balok.
$$\begin{aligned} V & = p \ell t \\ & = 10(30)(50) \\ & = 15.000~\text{cm}^3 \end{aligned}$$Jadi, volume balok tersebut adalah $\boxed{15.000~\text{cm}^3}$
(Jawaban D)
Soal Nomor 4
Jumlah panjang jari-jari alas dan tinggi suatu tabung adalah $37$ meter. Jika luas permukaan tabung itu adalah $1.628~\text{m}^2$ dan asumsikan $\pi = \dfrac{22}{7}$, maka volume tabung adalah ....
A. $660~\text{m}^3$
B. $2.310~\text{m}^3$
C. $4.620~\text{m}^3$
D. $9.240~\text{m}^3$
E. $32.340~\text{m}^3$
Pembahasan :
Diketahui $r + t = 37~\text{m}$ dan $L_p = 1.628~\text{m}^2.$
Pertama, akan dicari panjang jari-jari alas tabung.
$$\begin{aligned} L_p & = 1.628 \\ 2 \pi r(\color{blue}{r + t}) & = 1.628 \\ 2 \cdot \dfrac{22}{7} \cdot r(37) & = 1.628 \\ r & = \dfrac{1.628 \cdot 7}{2 \cdot 37 \cdot 22} \\ r & =
7~\text{m} \end{aligned}$$Karena $r + t = 37~\text{m}$ dan $r =7~\text{m}$, maka $t = 30~\text{m}$. Dengan demikian,
$$\begin{aligned} V & = \pi r^2 t \\ & = \dfrac{22}{7}\cdot 7^2 \cdot 30 \\ & = 4.620~\text{m}^3 \end{aligned}$$Jadi, volume tabung tersebut adalah $\boxed{4.620~\text{cm}^3}$
(Jawaban C)
Soal Nomor 5
Rasio luas permukaan dan luas selimut sebuah tabung yang alasnya berjari-jari $80~\text{cm}$ dan tingginya $20~\text{cm}$ adalah $\cdots\cdot$
A. $3 : 1$
B. $4 : 1$
C. $5 : 1$
D. $10 : 1$
E. $12 : 1$
Pembahasan :
Diketahui $r = 80~\text{cm}$ dan $t = 20~\text{cm}.$
Perbandingan (rasio) luas permukaan dan luas selimut tabung
dinyatakan sebagai berikut.
$$\begin{aligned} L_p : L_s & = \cancel{2\pi r}(r + t) :
\cancel{2\pi r} t \\ & = (r + t) : t \\ & = (80 + 20) : 20
\\ & = 100 : 20 \\ & = 5 : 1 \end{aligned}$$Jadi, rasio luas
permukaan dan luas selimut tabung tersebut adalah $\boxed{5 :1}$
(Jawaban C)
Soal Nomor 6
Dua buah tabung yang bervolume sama mempunyai tinggi dengan perbandingan $1 : 2$. Perbandingan panjang jari-jari kedua tabung tersebut adalah $\cdots \cdot$
A. $1 : \sqrt2$
B. $\sqrt2 : 1$
C. $1 : 2$
D. $2 : 1$
E. $2\sqrt2 : 1$
Pembahasan :
Misalkan tabung pertama memiliki panjang jari-jari, tinggi, dan
volume berturut-turut $r, t$, dan $V$, sedangkan tabung kedua
memiliki panjang jari-jari, tinggi, dan volume berturut-turut $r’,
t’$, dan $V’$ sehingga diperoleh hubungan
$$\begin{aligned} V’ & = V \\ t : t’ = 1 : 2 \Rightarrow t’
& = 2t \end{aligned}$$Karena itu, kita dapatkan
$$\begin{aligned} \pi(r’)^2t’ & = \pi r^2t \\ (r’)^2 (2t) &
= r^2t \\ 2(r’)^2 & = r^2 \\ 2 & =
\left(\dfrac{r}{r’}\right)^2 \\ \sqrt2 & = \dfrac{r}{r’}
\end{aligned}$$Jadi, perbandingan panjang jari-jari kedua tabung itu adalah $\boxed{\sqrt2 : 1}$
(Jawaban B)
Soal Nomor 7
Rasio antara luas selimut dan luas permukaan sebuah tabung adalah $1 : 2$. Jika luas permukaan tabung $616~\text{cm}^2$ dan asumsikan $\pi = \dfrac{22}{7}$, maka volume tabung tersebut adalah $\cdots \cdot$
A. $539~\text{cm}^3$
B. $1.078~\text{cm}^3$
C. $1.617~\text{cm}^3$
D. $2.156~\text{cm}^3$
E. $4.312~\text{cm}^3$
Pembahasan :
Diketahui:
$\begin{aligned} L_s : L_p & = 1 : 2 \\ L_p & =
616~\text{cm}^2 \end{aligned}$
Dari perbandingan tersebut, diperoleh
$$\begin{aligned} L_s & = \dfrac12 \cdot 616 \\ & =
308~\text{cm}^2 \end{aligned}$$Berikutnya, akan dicari panjang
jari-jari alas tabung.
$$\begin{aligned} L_p & = 616 \\ 2\pi r^2 + L_s & = 616 \\
2 \cdot \dfrac{22}{7}r^2 + 308 & = 616 \\ \dfrac{44}{7}r^2 &
= 308 \\ r^2 & = 49 \\ r & = 7~\text{cm}
\end{aligned}$$Dengan demikian,
$$\begin{aligned} L_s & = 308 \\ 2\pi r t & = 308 \\ t
& = \dfrac{308}{2\pi r}~\text{cm} \end{aligned}$$Selanjutnya,
volume tabung $V$ dihitung sebagai berikut.
$$\begin{aligned} V & = \pi r^2 t \\ & = \pi r^2 \cdot
\dfrac{308}{2\pi r} \\ & = 154r \\ & = 154(7) =
1.078~\text{cm}^3 \end{aligned}$$Jadi, volume tabung tersebut adalah
$\boxed{1.078~\text{cm}^3}$
(Jawaban B)
Soal Nomor 8
Jika tinggi suatu kerucut dikalikan dua, maka persentase pertambahan
volume kerucut sebesar $\cdots \cdot$
A. $25\%$
B. $50\%$
C. $100\%$
D. $200\%$
E. $400\%$
Pembahasan :
Anggap $r, t$, dan $V$ berturut-turut adalah panjang jari-jari
alas, tinggi, dan volume kerucut sehingga $V = \dfrac13\pi r^2t$.
Misalkan $t’$ adalah tinggi kerucut setelah dikalikan dua, maka $t’
= 2t$ sehingga volume setelahnya dinyatakan oleh
$$\begin{aligned} V’ & = \dfrac13\pi r^3 t’ \\ & =
\dfrac13\pi r^3 (2t) \\ & = 2\left(\dfrac13\pi r^3 t’\right) \\
& = 2V \end{aligned}$$Ini menunjukkan bahwa volumenya sama
dengan 2 kali volume awal. Dengan kata lain, persentase pertambahan
volumenya sebesar $\boxed{100\%}$
(Jawaban C)
Soal Nomor 9
Rasio volume 2 buah kerucut adalah $1 : 4$ dan rasio antardiameternya
$4 : 5$. Rasio tinggi kedua kerucut tersebut adalah $\cdots \cdot$
A. $9 : 16$
B. $16 : 25$
C. $25 : 36$
D. $25 : 64$
E. $25 : 81$
Pembahasan :
Anggap $r_1, t_1$, dan $V_1$ berturut-turut adalah panjang
jari-jari alas, tinggi, dan volume kerucut pertama sehingga $V_1 =
\dfrac13\pi r_1^2t_1$, sedangkan $r_2, t_2$, dan $V_2$
berturut-turut adalah panjang jari-jari alas, tinggi, dan volume
kerucut kedua sehingga $V_2 = \dfrac13\pi r_2^2t_2$. Dengan
demikian, dapat kita tuliskan perbandingan berikut.
$$\begin{aligned} V_1 : V_2 & = \color{red}{\dfrac13\pi}
r_1^2t_1 : \color{red}{\dfrac13\pi} r_2^2t_2 \\ V_1 : V_2 & =
r_1^2t_1 : r_2^2t_2 \\ 1 : 4 & = (4)^2t_1 : (5)^2t_2 \\ 1 : 4
& = 16t_1 : 25t_2 \\ \dfrac14 & = \dfrac{16t_1}{25t_2} \\
\dfrac{25}{64} & = \dfrac{t_1}{t_2} \\ 25 : 64 & = t_1 : t_2
\end{aligned}$$Jadi, rasio tinggi kedua kerucut tersebut adalah
$\boxed{25 : 64}$
(Jawaban D)
Soal Nomor 10
Jika rasio tinggi kerucut adalah $1 : 4$ dan rasio panjang
jari-jari alasnya $4 : 1$, maka rasio volume kedua kerucut itu adalah
$\cdots \cdot$
A. $1 : 4$
B. $2 : 1$
C. $4 : 1$
D. $8 : 1$
E. $16 : 1$
Anggap $r, t$, dan $V$ berturut-turut adalah panjang jari-jari
alas, tinggi, dan volume kerucut sehingga $V = \dfrac13\pi r^2t$.
Misalkan $t’$ adalah tinggi kerucut setelah dikalikan dua, maka $t’
= 2t$ sehingga volume setelahnya dinyatakan oleh
$$\begin{aligned} V’ & = \dfrac13\pi r^3 t’ \\ & =
\dfrac13\pi r^3 (2t) \\ & = 2\left(\dfrac13\pi r^3 t’\right) \\
& = 2V \end{aligned}$$Ini menunjukkan bahwa volumenya sama
dengan 2 kali volume awal. Dengan kata lain, persentase pertambahan
volumenya sebesar $\boxed{100\%}$
(Jawaban C)
Soal Nomor 9
Rasio volume 2 buah kerucut adalah $1 : 4$ dan rasio antardiameternya
$4 : 5$. Rasio tinggi kedua kerucut tersebut adalah $\cdots \cdot$
A. $9 : 16$
B. $16 : 25$
C. $25 : 36$
D. $25 : 64$
E. $25 : 81$
Pembahasan :
Anggap $r_1, t_1$, dan $V_1$ berturut-turut adalah panjang
jari-jari alas, tinggi, dan volume kerucut pertama sehingga $V_1 =
\dfrac13\pi r_1^2t_1$, sedangkan $r_2, t_2$, dan $V_2$
berturut-turut adalah panjang jari-jari alas, tinggi, dan volume
kerucut kedua sehingga $V_2 = \dfrac13\pi r_2^2t_2$. Dengan
demikian, dapat kita tuliskan perbandingan berikut.
$$\begin{aligned} V_1 : V_2 & = \color{red}{\dfrac13\pi}
r_1^2t_1 : \color{red}{\dfrac13\pi} r_2^2t_2 \\ V_1 : V_2 & =
r_1^2t_1 : r_2^2t_2 \\ 1 : 4 & = (4)^2t_1 : (5)^2t_2 \\ 1 : 4
& = 16t_1 : 25t_2 \\ \dfrac14 & = \dfrac{16t_1}{25t_2} \\
\dfrac{25}{64} & = \dfrac{t_1}{t_2} \\ 25 : 64 & = t_1 : t_2
\end{aligned}$$Jadi, rasio tinggi kedua kerucut tersebut adalah
$\boxed{25 : 64}$
(Jawaban D)
Soal Nomor 10
Jika rasio tinggi kerucut adalah $1 : 4$ dan rasio panjang
jari-jari alasnya $4 : 1$, maka rasio volume kedua kerucut itu adalah
$\cdots \cdot$
A. $1 : 4$
B. $2 : 1$
C. $4 : 1$
D. $8 : 1$
E. $16 : 1$
Pembahasan :
Diketahui $t_1 : t_2 = 1 : 4$ dan $r_1 : r_2 = 4 : 1$. Perbandingan
(rasio) kedua kerucut itu dinyatakan oleh $V_1 : V_2$, yaitu sebagai
berikut.
$$\begin{aligned} V_1 : V_2 & = \color{red}{\dfrac13\pi} r_1^2
t_1 : \color{red}{\dfrac13\pi} r_2^2 t_2 \\ & = r_1^2 t_1 :
r_2^2 t_2 \\ & = (4)^2(1) : (1)^2(4) \\ & = 4 : 1
\end{aligned}$$Jadi, rasio kedua volume kerucut itu adalah $\boxed{4
: 1}$
(Jawaban C)
Soal Nomor 11
Sebuah tabung yang terbuat dari besi cor (padat) dengan panjang
jari-jari alas $3~\text{cm}$ dan tinggi $5~\text{cm}$ dilebur. Hasil
leburan digunakan untuk membuat $n$ buah kerucut padat dengan panjang
jari-jari alas $1~\text{mm}$ dan tinggi $1~\text{cm}$. Asumsikan semua
besi cor terpakai. Nilai $n$ adalah $\cdots \cdot$
A. $1.500$
B. $4.500$
C. $9.000$
D. $13.500$
E. $40.500$
Pembahasan :
Diketahui:
$$\begin{aligned} r_{\text{tabung}} & = 3~\text{cm} \\
t_{\text{tabung}} & = 5~\text{cm} \\ r_{\text{kerucut}} & =
1~\text{mm} = 0,1~\text{cm} \\ t_{\text{kerucut}} & =
1~\text{cm} \end{aligned}$$Banyaknya kerucut yang terbentuk dari
hasil peleburan tabung tersebut sama dengan volume tabung dibagi
dengan volume kerucut.
$$\begin{aligned} n & =
\dfrac{V_{\text{tabung}}}{V_{\text{kerucut}}} \\ & =
\dfrac{\color{red}{\pi} r_{\text{tabung}}^2
t_{\text{tabung}}}{\frac13\color{red}{\pi} r_{\text{kerucut}}^2
t_{\text{kerucut}}} \\ & = \dfrac{3^2 \cdot 5}{\frac13 \cdot
0,1^2 \cdot 1} \\ & = \dfrac{45}{\frac{1}{300}} = 45 \cdot 300 =
13.500 \end{aligned}$$Jadi, nilai $\boxed{n = 13.500}$
(Jawaban D)
Soal Nomor 12
Jika sebuah bola dimasukkan ke dalam kubus, maka perbandingan volume
bola terbesar terhadap volume kubus adalah $\cdots \cdot$
A. $\pi : 3$
B. $\pi : 4$
C. $\pi : 6$
D. $2\pi : 3$
E. $2\pi : 5$
$$\begin{aligned} r_{\text{tabung}} & = 3~\text{cm} \\
t_{\text{tabung}} & = 5~\text{cm} \\ r_{\text{kerucut}} & =
1~\text{mm} = 0,1~\text{cm} \\ t_{\text{kerucut}} & =
1~\text{cm} \end{aligned}$$Banyaknya kerucut yang terbentuk dari
hasil peleburan tabung tersebut sama dengan volume tabung dibagi
dengan volume kerucut.
$$\begin{aligned} n & =
\dfrac{V_{\text{tabung}}}{V_{\text{kerucut}}} \\ & =
\dfrac{\color{red}{\pi} r_{\text{tabung}}^2
t_{\text{tabung}}}{\frac13\color{red}{\pi} r_{\text{kerucut}}^2
t_{\text{kerucut}}} \\ & = \dfrac{3^2 \cdot 5}{\frac13 \cdot
0,1^2 \cdot 1} \\ & = \dfrac{45}{\frac{1}{300}} = 45 \cdot 300 =
13.500 \end{aligned}$$Jadi, nilai $\boxed{n = 13.500}$
(Jawaban D)
Soal Nomor 12
Jika sebuah bola dimasukkan ke dalam kubus, maka perbandingan volume
bola terbesar terhadap volume kubus adalah $\cdots \cdot$
A. $\pi : 3$
B. $\pi : 4$
C. $\pi : 6$
D. $2\pi : 3$
E. $2\pi : 5$
Pembahasan :
Volume bola terbesar tercapai ketika panjang diameter bolanya sama
dengan panjang rusuk kubus sehingga bola tepat bersinggungan dengan
seluruh sisi kubus. Jika $s$ dan $r$ berturut-turut adalah panjang
rusuk kubus dan panjang jari-jari bola, maka diperoleh hubungan $s =
d = 2r$. Dengan demikian, perbandingan volumenya dinyatakan sebagai
berikut.
$$\begin{aligned} V_{\text{bola}} : V_{\text{kubus}} & =
\dfrac43\pi r^3 : s^3 \\ & = \dfrac43\pi r^3 : (2r)^3 \\ & =
\dfrac43\pi \color{red}{r^3} : 8\color{red}{r^3} \\ & =
\dfrac43\pi : 8 \\ & = \pi : 6 && (\text{Dikali 3/4})
\end{aligned}$$Jadi, perbandingan volume bola terbesar terhadap
volume kubus adalah $\boxed{\pi : 6}$
(Jawaban C)
Soal Nomor 13
Sebuah bola berjari-jari $5\sqrt3~\text{cm}$. Volume kubus terbesar
yang berada di dalam bola itu adalah $....$
A. $125~\text{cm}^3$
B. $375~\text{cm}^3$
C. $500~\text{cm}^3$
D. $1.000~\text{cm}^3$
E. $3.000~\text{cm}^3$
Pembahasan :
Volume bola terbesar tercapai ketika panjang diameter bolanya sama
dengan panjang rusuk kubus sehingga bola tepat bersinggungan dengan
seluruh sisi kubus. Jika $s$ dan $r$ berturut-turut adalah panjang
rusuk kubus dan panjang jari-jari bola, maka diperoleh hubungan $s =
d = 2r$. Dengan demikian, perbandingan volumenya dinyatakan sebagai
berikut.
$$\begin{aligned} V_{\text{bola}} : V_{\text{kubus}} & =
\dfrac43\pi r^3 : s^3 \\ & = \dfrac43\pi r^3 : (2r)^3 \\ & =
\dfrac43\pi \color{red}{r^3} : 8\color{red}{r^3} \\ & =
\dfrac43\pi : 8 \\ & = \pi : 6 && (\text{Dikali 3/4})
\end{aligned}$$Jadi, perbandingan volume bola terbesar terhadap
volume kubus adalah $\boxed{\pi : 6}$
(Jawaban C)
Soal Nomor 13
Sebuah bola berjari-jari $5\sqrt3~\text{cm}$. Volume kubus terbesar
yang berada di dalam bola itu adalah $....$
A. $125~\text{cm}^3$
B. $375~\text{cm}^3$
C. $500~\text{cm}^3$
D. $1.000~\text{cm}^3$
E. $3.000~\text{cm}^3$
Pembahasan :
Kubus terbesar itu
memiliki panjang diagonal ruang yang sama dengan
panjang diameter bola, seperti yang tampak pada gambar.
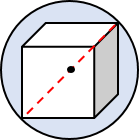
Karena bolanya berjari-jari $r = 5\sqrt3~\text{cm}$, maka $d = 2r
= 10\sqrt3~\text{cm}.$
Panjang diagonal ruang kubus yang panjang rusuknya $a$ adalah $DR =
a\sqrt3~\text{cm}$ sehingga
$$\begin{aligned} DR & = d \\ a\sqrt3 & = 10\sqrt3 \\ a
& = 10~\text{cm} \end{aligned}$$Volume kubus tersebut adalah
$\boxed{V = a^3 = (10)^3 = 1.000~\text{cm}^3}$
(Jawaban D)
Soal Nomor 14
Jika panjang jari-jari suatu bola adalah $x~\text{cm}$, maka
perbandingan luas permukaan bola padat utuh, setengah bola padat, dan
seperempat bola padat itu adalah $\cdots \cdot$
A. $6 : 3 : 2$
B. $4 : 3 : 2$
C. $4 : 3 : 1$
D. $4 : 2 : 1$
E. $3 : 2 : 1$
Pembahasan :
panjang diameter bola, seperti yang tampak pada gambar.

Karena bolanya berjari-jari $r = 5\sqrt3~\text{cm}$, maka $d = 2r
= 10\sqrt3~\text{cm}.$
Panjang diagonal ruang kubus yang panjang rusuknya $a$ adalah $DR =
a\sqrt3~\text{cm}$ sehingga
$$\begin{aligned} DR & = d \\ a\sqrt3 & = 10\sqrt3 \\ a
& = 10~\text{cm} \end{aligned}$$Volume kubus tersebut adalah
$\boxed{V = a^3 = (10)^3 = 1.000~\text{cm}^3}$
(Jawaban D)
Soal Nomor 14
Jika panjang jari-jari suatu bola adalah $x~\text{cm}$, maka
perbandingan luas permukaan bola padat utuh, setengah bola padat, dan
seperempat bola padat itu adalah $\cdots \cdot$
A. $6 : 3 : 2$
B. $4 : 3 : 2$
C. $4 : 3 : 1$
D. $4 : 2 : 1$
E. $3 : 2 : 1$
Pembahasan :
Perhatikan sketsa gambar bola, setengah bola, dan seperempat bola
berikut.
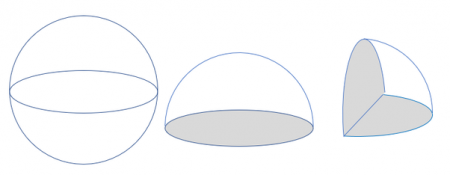
Luas permukaan bola padat (pejal) utuh adalah $$L_{\oplus} = 4\pi
r^2.$$Luas permukaan setengah bola padat adalah penjumlahan dari luas
kulit ditambah dengan luas lingkaran dalamannya (ditandai dengan warna
abu-abu pada gambar), yaitu $$L_{\frac12 \oplus} =
2\pi r^2 + \pi r^2 = 3\pi r^2.$$Luas permukaan seperempat bola padat
adalah penjumlahan dari luas kulit ditambah 2 kali luas setengah
lingkaran dalamannya, yaitu $$L_{\frac14 \oplus} = \pi r^2 + \dfrac12
\pi r^2 + \dfrac12 \pi r^2 = 2\pi r^2.$$Jadi, perbandingan luas
permukaan bola padat utuh, setengah bola padat, dan seperempat bola
padat itu adalah
$$\begin{aligned} L_{\oplus} : L_{\frac12 \oplus} : L_{\frac14 \oplus}
& = 4\color{red}{\pi r^2} : 3\color{red}{\pi r^2} : 2\color{red}{\pi
r^2} \\ & = 4 : 3 : 2 \end{aligned}$$(Jawaban B).
Jika masing-masing rusuk sebuah kubus bertambah $50\%$, hitunglah
persentase pertambahan untuk:
a. luas permukaan kubus;
b. volume kubus.
Pembahasan :
berikut.

Luas permukaan bola padat (pejal) utuh adalah $$L_{\oplus} = 4\pi
r^2.$$Luas permukaan setengah bola padat adalah penjumlahan dari luas
kulit ditambah dengan luas lingkaran dalamannya (ditandai dengan warna
abu-abu pada gambar), yaitu $$L_{\frac12 \oplus} =
2\pi r^2 + \pi r^2 = 3\pi r^2.$$Luas permukaan seperempat bola padat
adalah penjumlahan dari luas kulit ditambah 2 kali luas setengah
lingkaran dalamannya, yaitu $$L_{\frac14 \oplus} = \pi r^2 + \dfrac12
\pi r^2 + \dfrac12 \pi r^2 = 2\pi r^2.$$Jadi, perbandingan luas
permukaan bola padat utuh, setengah bola padat, dan seperempat bola
padat itu adalah
$$\begin{aligned} L_{\oplus} : L_{\frac12 \oplus} : L_{\frac14 \oplus}
& = 4\color{red}{\pi r^2} : 3\color{red}{\pi r^2} : 2\color{red}{\pi
r^2} \\ & = 4 : 3 : 2 \end{aligned}$$(Jawaban B).
BAGIAN URAIAN
Soal Nomor 1Jika masing-masing rusuk sebuah kubus bertambah $50\%$, hitunglah
persentase pertambahan untuk:
a. luas permukaan kubus;
b. volume kubus.
Pembahasan :
Mula-mula panjang rusuk kubus adalah $s$, kemudian bertambah
menjadi $s’ = 150\%s$.
Jawaban a)
Mula-mula luas permukaan kubus adalah $L = 6s$. Luas permukaan
kubus setelah pemanjangan panjang rusuk dinyatakan oleh
$$\begin{aligned} L’ & = 6s’ \\ & = 6(150\%s) \\ & =
150\%(6s) \\ & = 150\%L \end{aligned}$$Jadi, persentase
pertambahan luas permukaan kubus adalah $\boxed{50\%}$
Jawaban b)
Mula-mula volume kubus adalah $V = s^3$. Volume setelah pemanjangan
panjang rusuk dinyatakan oleh
$$\begin{aligned} V’ & = (s’)^3 \\ & = (150\%s)^3 \\ &
= 337,5\%s^3 \end{aligned}$$Jadi, persentase pertambahan volume
kubus adalah $\boxed{237,5\%}$
Soal Nomor 2
Jika $V$ merupakan volume dan $S$ merupakan luas permukaan balok yang
berukuran $a \times b \times c$, buktikan bahwa $\dfrac{1}{V} =
\dfrac{2}{S}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right).$
Pembahasan :
menjadi $s’ = 150\%s$.
Jawaban a)
Mula-mula luas permukaan kubus adalah $L = 6s$. Luas permukaan
kubus setelah pemanjangan panjang rusuk dinyatakan oleh
$$\begin{aligned} L’ & = 6s’ \\ & = 6(150\%s) \\ & =
150\%(6s) \\ & = 150\%L \end{aligned}$$Jadi, persentase
pertambahan luas permukaan kubus adalah $\boxed{50\%}$
Jawaban b)
Mula-mula volume kubus adalah $V = s^3$. Volume setelah pemanjangan
panjang rusuk dinyatakan oleh
$$\begin{aligned} V’ & = (s’)^3 \\ & = (150\%s)^3 \\ &
= 337,5\%s^3 \end{aligned}$$Jadi, persentase pertambahan volume
kubus adalah $\boxed{237,5\%}$
Soal Nomor 2
Jika $V$ merupakan volume dan $S$ merupakan luas permukaan balok yang
berukuran $a \times b \times c$, buktikan bahwa $\dfrac{1}{V} =
\dfrac{2}{S}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right).$
Pembahasan :
Pada balok berukuran $a \times b \times c$, volume dan luas
permukaannya dinyatakan oleh
$$\begin{aligned} V & = abc \\ S & = 2(ab + ac + bc)
\end{aligned}$$Akan dibuktikan bahwa $\dfrac{1}{V} =
\dfrac{2}{S}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)$
dimulai dari ruas kanan.
$$\begin{aligned}
\dfrac{2}{S}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)
& = \dfrac{2}{2(ab + ac + bc)}\left(\dfrac{bc}{abc} +
\dfrac{ac}{abc} + \dfrac{ab}{abc}\right) \\ & =
\dfrac{1}{\cancel{ab + ac + bc}} \cdot \dfrac{\cancel{ab + ac +
bc}}{abc} \\ & = \dfrac{1}{abc} \\ & = \dfrac{1}{V}
\end{aligned}$$Jadi, terbukti bahwa $\boxed{\dfrac{1}{V} =
\dfrac{2}{S}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)}$
Soal Nomor 3
Gambar berikut menunjukkan pelat besi yang berbentuk kotak persegi
panjang dengan salah satu bidangnya $FDCBGE$ dapat bergerak
buka-tutup.
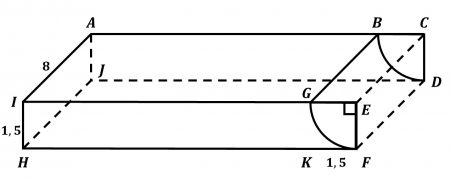
Lengkungan $FG$ merupakan seperempat dari keliling lingkaran yang
pusatnya di $E$. Diketahui $KF = 1,5~\text{cm}$, $HK = 5~\text{cm}$, $HI
= 1,5~\text{cm}$, dan $AI = 8~\text{cm}$.
permukaannya dinyatakan oleh
$$\begin{aligned} V & = abc \\ S & = 2(ab + ac + bc)
\end{aligned}$$Akan dibuktikan bahwa $\dfrac{1}{V} =
\dfrac{2}{S}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)$
dimulai dari ruas kanan.
$$\begin{aligned}
\dfrac{2}{S}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)
& = \dfrac{2}{2(ab + ac + bc)}\left(\dfrac{bc}{abc} +
\dfrac{ac}{abc} + \dfrac{ab}{abc}\right) \\ & =
\dfrac{1}{\cancel{ab + ac + bc}} \cdot \dfrac{\cancel{ab + ac +
bc}}{abc} \\ & = \dfrac{1}{abc} \\ & = \dfrac{1}{V}
\end{aligned}$$Jadi, terbukti bahwa $\boxed{\dfrac{1}{V} =
\dfrac{2}{S}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)}$
Soal Nomor 3
Gambar berikut menunjukkan pelat besi yang berbentuk kotak persegi
panjang dengan salah satu bidangnya $FDCBGE$ dapat bergerak
buka-tutup.

Lengkungan $FG$ merupakan seperempat dari keliling lingkaran yang
pusatnya di $E$. Diketahui $KF = 1,5~\text{cm}$, $HK = 5~\text{cm}$, $HI
= 1,5~\text{cm}$, dan $AI = 8~\text{cm}$.
Hitunglah:
a. luas $HKFGI$,
b. volume pelat besi,
c. luas selimut $FDBG$, dan
a. luas $HKFGI$,
b. volume pelat besi,
c. luas selimut $FDBG$, dan
d. massa benda itu apabila massa jenis besi $9.040~\text{kg/m}^3 (\pi = 3,14).$
Pembahasan :
Jawaban a)
Luas $HKFGI$ sama dengan luas persegi panjang $HFEI$ dikurangi luas
seperempat lingkaran $FEG$.
$$\begin{aligned} L_{HKFGI} & = L_{HFEI}-L_{FEG} \\ & = (HF
\cdot FE)-\left(\dfrac14 \cdot \pi \cdot EF^2\right) \\ & = (6,5
\cdot 1,5)-\left(\dfrac14 \cdot 3.14 \cdot 1,5^2\right) \\ & =
9,75-1,76625 \\ & = 7,98375~\text{cm}^2 \end{aligned}$$Jadi,
luas $HKFGI$ adalah $\boxed{7,98375~\text{cm}^2}$
Jawaban b)
Volume pelat besi sama dengan volume balok $HFDJ.IECA$ dikurangi
volume seperempat tabung $FEG.DCB$.
$$\begin{aligned} V_{\text{pelat besi}} & =
V_{HFDJ.IECA}-V_{FEG.DCB} \\ & = (HF \cdot HI \cdot
AI)-\left(\dfrac14 \cdot \pi \cdot EF^2 \cdot EC\right) \\ & =
(6,5 \cdot 1,5 \cdot 8)-\left(\dfrac14 \cdot 3,14 \cdot 1,5^2 \cdot
8\right) \\ & = 78-14,13 \\ & = 63,87~\text{cm}^3
\end{aligned}$$Jadi, volume pelat besi adalah
$\boxed{63,87~\text{cm}^3}$
Jawaban c)
Luas selimut $FDBG$ sama dengan luas persegi panjang $FDCE$
ditambah luas persegi panjang $ECBG$.
$$\begin{aligned} L_{FDBG} & = L_{FDCE} + L_{ECBG} \\ & =
(FD \cdot DC) + (GE \cdot EC) \\ & = (8 \cdot 1,5) + (1,5 \cdot
8) \\ & = 12 + 12 = 24~\text{cm}^2 \end{aligned}$$Jadi, luas
selimut $FDBG$ adalah $\boxed{24~\text{cm}^2}$
Jawaban d)
Karena volume pelat besi adalah $V = 63,87~\text{cm}^3$ dan
diketahui bahwa $\rho = 9.040~\text{kg/m}^3 = 9,04~\text{g/cm}^3$
maka massa pelat besi dapat kita tentukan sebagai berikut.
$$\begin{aligned} \rho & = \dfrac{m}{V} \\ m & = \rho \cdot
V \\ & = 9,04 \cdot 63,87 \\ & = 577,3848~\text{g}
\end{aligned}$$Jadi, massa pelat besi adalah
$\boxed{577,3848~\text{g}}$
Soal Nomor 4
Struktur sebuah tempat pembuangan rokok terlihat seperti gambar
berikut.
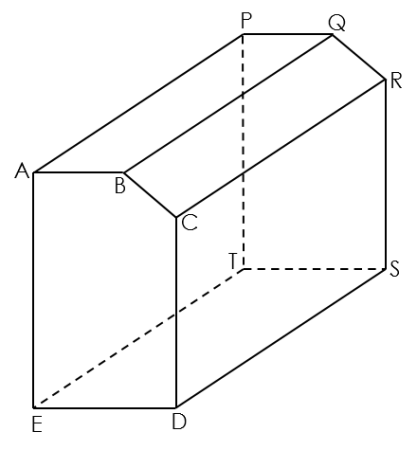
Pembahasan :
Pembahasan :
Jawaban a)
Luas $HKFGI$ sama dengan luas persegi panjang $HFEI$ dikurangi luas
seperempat lingkaran $FEG$.
$$\begin{aligned} L_{HKFGI} & = L_{HFEI}-L_{FEG} \\ & = (HF
\cdot FE)-\left(\dfrac14 \cdot \pi \cdot EF^2\right) \\ & = (6,5
\cdot 1,5)-\left(\dfrac14 \cdot 3.14 \cdot 1,5^2\right) \\ & =
9,75-1,76625 \\ & = 7,98375~\text{cm}^2 \end{aligned}$$Jadi,
luas $HKFGI$ adalah $\boxed{7,98375~\text{cm}^2}$
Jawaban b)
Volume pelat besi sama dengan volume balok $HFDJ.IECA$ dikurangi
volume seperempat tabung $FEG.DCB$.
$$\begin{aligned} V_{\text{pelat besi}} & =
V_{HFDJ.IECA}-V_{FEG.DCB} \\ & = (HF \cdot HI \cdot
AI)-\left(\dfrac14 \cdot \pi \cdot EF^2 \cdot EC\right) \\ & =
(6,5 \cdot 1,5 \cdot 8)-\left(\dfrac14 \cdot 3,14 \cdot 1,5^2 \cdot
8\right) \\ & = 78-14,13 \\ & = 63,87~\text{cm}^3
\end{aligned}$$Jadi, volume pelat besi adalah
$\boxed{63,87~\text{cm}^3}$
Jawaban c)
Luas selimut $FDBG$ sama dengan luas persegi panjang $FDCE$
ditambah luas persegi panjang $ECBG$.
$$\begin{aligned} L_{FDBG} & = L_{FDCE} + L_{ECBG} \\ & =
(FD \cdot DC) + (GE \cdot EC) \\ & = (8 \cdot 1,5) + (1,5 \cdot
8) \\ & = 12 + 12 = 24~\text{cm}^2 \end{aligned}$$Jadi, luas
selimut $FDBG$ adalah $\boxed{24~\text{cm}^2}$
Jawaban d)
Karena volume pelat besi adalah $V = 63,87~\text{cm}^3$ dan
diketahui bahwa $\rho = 9.040~\text{kg/m}^3 = 9,04~\text{g/cm}^3$
maka massa pelat besi dapat kita tentukan sebagai berikut.
$$\begin{aligned} \rho & = \dfrac{m}{V} \\ m & = \rho \cdot
V \\ & = 9,04 \cdot 63,87 \\ & = 577,3848~\text{g}
\end{aligned}$$Jadi, massa pelat besi adalah
$\boxed{577,3848~\text{g}}$
Soal Nomor 4
Struktur sebuah tempat pembuangan rokok terlihat seperti gambar
berikut.

Pembahasan :
Diketahui:
$$\begin{aligned} AB & = PQ = 90~\text{cm} \\ ED & = TS =
120~\text{cm} \\ AE & = PT = 220~\text{cm} \\ CD & = RS =
180~\text{cm} \\ AP & = BQ = CR = DS = ET = 200~\text{cm}
\end{aligned}$$Hitunglah:
panjang $BC$,
luas $ABCDE$, dan
volume tempat rokok tersebut dalam satuan meter kubik.
Jawaban a)
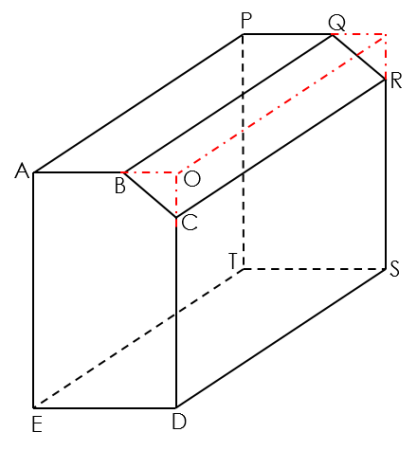
Buat titik $O$, sedemikian sehingga $AO \perp OD$ dan terbentuklah
segitiga siku-siku $BOC$ dengan
$$\begin{aligned} BO & = AO-AB = 120-90 = 30~\text{cm} \\ OC
& = OD-CD = 220-180 = 40~\text{cm} \end{aligned}$$Dengan
menggunakan rumus Phytagoras, diperoleh
$$\begin{aligned} BC & = \sqrt{BO^2 + OC^2} \\ & =
\sqrt{30^2 + 40^2} \\ & = 50~\text{cm} \end{aligned}$$Jadi,
paniang $\boxed{BC = 50~\text{cm}}$
Jawaban b)
Luas segilima $ABCDE$ sama dengan luas persegi panjang $AEDO$
dikurangi luas segitiga siku-siku $BOC$.
$$\begin{aligned} L_{ABCDE} & = L_{AEDO}-L_{\triangle BOC} \\
& = (AE \cdot ED)-\left(\dfrac12 \cdot BO \cdot OC\right) \\
& = (220 \cdot 120)-\left(\dfrac12 \cdot 30 \cdot 40\right) \\
& = 26.400-600 \\ & = 25.800~\text{cm}^2
\end{aligned}$$Jadi, luas $ABCDE$ adalah
$\boxed{25.800~\text{cm}^2}$
Jawaban c)
Volume benda tersebut sama dengan volume balok utuh dikurangi
volume prisma segitiga siku-siku hasil potongan.
$$\begin{aligned} V_{\text{benda}} & =
V_{\text{balok}}-V_{\text{prisma}} \\ & = (ED \cdot AE \cdot
AP)-\left(L_{\triangle BOC} \cdot BQ\right) \\ & = (120 \cdot
220 \cdot 200)-\left(600 \cdot 200\right) \\ & =
5.160.000~\text{cm}^3 \end{aligned}$$Jadi, volume tempat pembuangan
rokok tersebut adalah $\boxed{5.160.000~\text{cm}^3}$
Soal Nomor 5
Jika panjang jari-jari alas sebuah tabung bertambah $50\%$ dan
tingginya berkurang dengan rasio $4 : 9$, bagaimana volume tabung itu
sekarang?
Pembahasan :
$$\begin{aligned} AB & = PQ = 90~\text{cm} \\ ED & = TS =
120~\text{cm} \\ AE & = PT = 220~\text{cm} \\ CD & = RS =
180~\text{cm} \\ AP & = BQ = CR = DS = ET = 200~\text{cm}
\end{aligned}$$Hitunglah:
panjang $BC$,
luas $ABCDE$, dan
volume tempat rokok tersebut dalam satuan meter kubik.
Jawaban a)

Buat titik $O$, sedemikian sehingga $AO \perp OD$ dan terbentuklah
segitiga siku-siku $BOC$ dengan
$$\begin{aligned} BO & = AO-AB = 120-90 = 30~\text{cm} \\ OC
& = OD-CD = 220-180 = 40~\text{cm} \end{aligned}$$Dengan
menggunakan rumus Phytagoras, diperoleh
$$\begin{aligned} BC & = \sqrt{BO^2 + OC^2} \\ & =
\sqrt{30^2 + 40^2} \\ & = 50~\text{cm} \end{aligned}$$Jadi,
paniang $\boxed{BC = 50~\text{cm}}$
Jawaban b)
Luas segilima $ABCDE$ sama dengan luas persegi panjang $AEDO$
dikurangi luas segitiga siku-siku $BOC$.
$$\begin{aligned} L_{ABCDE} & = L_{AEDO}-L_{\triangle BOC} \\
& = (AE \cdot ED)-\left(\dfrac12 \cdot BO \cdot OC\right) \\
& = (220 \cdot 120)-\left(\dfrac12 \cdot 30 \cdot 40\right) \\
& = 26.400-600 \\ & = 25.800~\text{cm}^2
\end{aligned}$$Jadi, luas $ABCDE$ adalah
$\boxed{25.800~\text{cm}^2}$
Jawaban c)
Volume benda tersebut sama dengan volume balok utuh dikurangi
volume prisma segitiga siku-siku hasil potongan.
$$\begin{aligned} V_{\text{benda}} & =
V_{\text{balok}}-V_{\text{prisma}} \\ & = (ED \cdot AE \cdot
AP)-\left(L_{\triangle BOC} \cdot BQ\right) \\ & = (120 \cdot
220 \cdot 200)-\left(600 \cdot 200\right) \\ & =
5.160.000~\text{cm}^3 \end{aligned}$$Jadi, volume tempat pembuangan
rokok tersebut adalah $\boxed{5.160.000~\text{cm}^3}$
Soal Nomor 5
Jika panjang jari-jari alas sebuah tabung bertambah $50\%$ dan
tingginya berkurang dengan rasio $4 : 9$, bagaimana volume tabung itu
sekarang?
Pembahasan :
Misalkan $r$ dan $t$ adalah panjang jari-jari dan tinggi tabung
mula-mula sehingga $V = \pi r^2 t$. Misalkan pula $r’$ dan $t’$
adalah paniang jari-jari dan tinggi tabung setelah mengalami
perubahan sehingga
$$\begin{aligned} r’ & = 150\%r = \dfrac32r \\ t’ & =
\dfrac49t \end{aligned}$$Dengan demikian, kita peroleh
$$\begin{aligned} V’ & = \pi (r’)^2 t’ \\ & = \pi
\left(\dfrac32r\right)^2 \cdot \dfrac49t \\ & = \pi \cdot
\dfrac94r^2 \cdot \dfrac49t \\ & = \pi r^2 t \\ & = V
\end{aligned}$$Jadi, dapat disimpulkan bahwa volume tabung sekarang
sama dengan volume tabung mula-mula (tetap/tidak berubah).
Soal Nomor 6
Diketahui sebuah tabung dengan keliling alas = volume tabung = $n$.
Tentukan luas permukaan tabung tersebut bila dinyatakan dalam $n$.
Pembahasan :
mula-mula sehingga $V = \pi r^2 t$. Misalkan pula $r’$ dan $t’$
adalah paniang jari-jari dan tinggi tabung setelah mengalami
perubahan sehingga
$$\begin{aligned} r’ & = 150\%r = \dfrac32r \\ t’ & =
\dfrac49t \end{aligned}$$Dengan demikian, kita peroleh
$$\begin{aligned} V’ & = \pi (r’)^2 t’ \\ & = \pi
\left(\dfrac32r\right)^2 \cdot \dfrac49t \\ & = \pi \cdot
\dfrac94r^2 \cdot \dfrac49t \\ & = \pi r^2 t \\ & = V
\end{aligned}$$Jadi, dapat disimpulkan bahwa volume tabung sekarang
sama dengan volume tabung mula-mula (tetap/tidak berubah).
Soal Nomor 6
Diketahui sebuah tabung dengan keliling alas = volume tabung = $n$.
Tentukan luas permukaan tabung tersebut bila dinyatakan dalam $n$.
Pembahasan :
Diketahui keliling alas = volume tabung = $n$ sehingga kita
tulis
$$\begin{aligned} 2\pi r & = \pi r^2 t = n && (\cdots
1) \\ \Rightarrow 2 & = rt && (\cdots
2)\end{aligned}$$Dari persamaan $2\pi r = n$, kita peroleh $r =
\dfrac{n}{2\pi}$. Dari persamaan $(2)$, didapat $t = \dfrac{2}{r} =
2 \cdot \dfrac{2\pi}{n} = \dfrac{4\pi}{n}.$
Selanjutnya, kita akan peroleh luas permukaan tabung sebagai
berikut.
$$\begin{aligned} L_p & = 2\pi r(r + t) \\ & =
n\left(\dfrac{n}{2\pi} + \dfrac{4\pi}{n}\right) \\ & =
\dfrac{n^2}{2\pi} + 4\pi \end{aligned}$$Jadi, luas permukaaan tabung
tersebut bila dinyatakan dalam $n$ adalah $\boxed{L_p =
\dfrac{n^2}{2\pi} + 4\pi}$
Soal Nomor 7
Jika $t, s$, dan $v$ berturut-turut menyatakan tinggi, luas selimut,
dan volume kerucut, tentukan nilai $(3\pi vt^3-s^2t^2 + 9v^2).$
Pembahasan :
tulis
$$\begin{aligned} 2\pi r & = \pi r^2 t = n && (\cdots
1) \\ \Rightarrow 2 & = rt && (\cdots
2)\end{aligned}$$Dari persamaan $2\pi r = n$, kita peroleh $r =
\dfrac{n}{2\pi}$. Dari persamaan $(2)$, didapat $t = \dfrac{2}{r} =
2 \cdot \dfrac{2\pi}{n} = \dfrac{4\pi}{n}.$
Selanjutnya, kita akan peroleh luas permukaan tabung sebagai
berikut.
$$\begin{aligned} L_p & = 2\pi r(r + t) \\ & =
n\left(\dfrac{n}{2\pi} + \dfrac{4\pi}{n}\right) \\ & =
\dfrac{n^2}{2\pi} + 4\pi \end{aligned}$$Jadi, luas permukaaan tabung
tersebut bila dinyatakan dalam $n$ adalah $\boxed{L_p =
\dfrac{n^2}{2\pi} + 4\pi}$
Soal Nomor 7
Jika $t, s$, dan $v$ berturut-turut menyatakan tinggi, luas selimut,
dan volume kerucut, tentukan nilai $(3\pi vt^3-s^2t^2 + 9v^2).$
Pembahasan :
Diketahui/dimisalkan bahwa
$$\begin{aligned} t & = \text{tinggi kerucut} \\ r & =
\text{panjang jari-jari alas kerucut} \\ s’ & = \text{panjang
garis pelukis} \\ s & = \text{luas selimut kerucut} = \pi r s’
\\ v & = \text{volume kerucut} = \dfrac13\pi r^2 t
\end{aligned}$$Dengan menggunakan rumus Pythagoras, diperoleh
$(s’)^2 = r^2+t^2$. Oleh karena itu, kita akan peroleh
$$\begin{aligned} 3\pi vt^3-s^2t^2 + 9v^2 & =
3\pi\left(\dfrac13\pi r^2t\right)t^3-(\pi r s’)^2t^2 +
9\left(\dfrac13\pi r^2t\right)^2 \\ & =
\pi^2r^2t^4-\pi^2r^2(r^2+t^2)t^2 + 9 \cdot \dfrac19\pi^2 r^4t^2 \\
& =
\color{red}{\pi^2r^2t^4}\color{blue}{-\pi^2r^4t^2}\color{red}{-\pi^2r^2t^4}+
\color{blue}{\pi^2 r^4t^2} \\ & = 0 \end{aligned}$$Jadi, nilai
dari $\boxed{3\pi vt^3-s^2t^2 + 9v^2 = 0}$
Soal Nomor 8
Sebuah kerucut yang terbuat dari kayu jati dipotong horizontal menjadi
tiga bagian dengan masing-masing potongan mempunyai tinggi yang sama,
seperti yang terlihat pada gambar.
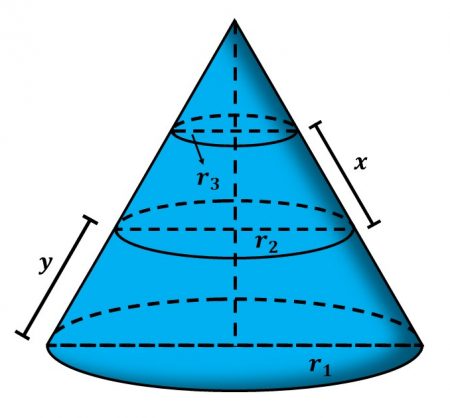
Tinggi kerucut sebelum dipotong adalah $42~\text{cm}$ dan panjang
jari-jari alas sebelum dipotong adalah $r_1 = 18~\text{cm}$.
Hitunglah:
Perbandingan volume masing-masing bagian, dan nilai $x$ dan $y$.
Pembahasan :
$$\begin{aligned} t & = \text{tinggi kerucut} \\ r & =
\text{panjang jari-jari alas kerucut} \\ s’ & = \text{panjang
garis pelukis} \\ s & = \text{luas selimut kerucut} = \pi r s’
\\ v & = \text{volume kerucut} = \dfrac13\pi r^2 t
\end{aligned}$$Dengan menggunakan rumus Pythagoras, diperoleh
$(s’)^2 = r^2+t^2$. Oleh karena itu, kita akan peroleh
$$\begin{aligned} 3\pi vt^3-s^2t^2 + 9v^2 & =
3\pi\left(\dfrac13\pi r^2t\right)t^3-(\pi r s’)^2t^2 +
9\left(\dfrac13\pi r^2t\right)^2 \\ & =
\pi^2r^2t^4-\pi^2r^2(r^2+t^2)t^2 + 9 \cdot \dfrac19\pi^2 r^4t^2 \\
& =
\color{red}{\pi^2r^2t^4}\color{blue}{-\pi^2r^4t^2}\color{red}{-\pi^2r^2t^4}+
\color{blue}{\pi^2 r^4t^2} \\ & = 0 \end{aligned}$$Jadi, nilai
dari $\boxed{3\pi vt^3-s^2t^2 + 9v^2 = 0}$
Soal Nomor 8
Sebuah kerucut yang terbuat dari kayu jati dipotong horizontal menjadi
tiga bagian dengan masing-masing potongan mempunyai tinggi yang sama,
seperti yang terlihat pada gambar.

Tinggi kerucut sebelum dipotong adalah $42~\text{cm}$ dan panjang
jari-jari alas sebelum dipotong adalah $r_1 = 18~\text{cm}$.
Hitunglah:
Perbandingan volume masing-masing bagian, dan nilai $x$ dan $y$.
Pembahasan :
Tampak pada gambar ada $3$ buah kerucut: besar, sedang, dan kecil.
Misalkan tinggi kerucut besar, sedang, dan kecil berturut-turut
adalah $t_1, t_2$, dan $t_3$ sehingga $t_1 = 42~\text{cm}$, $t_2 =
28~\text{cm}$, dan $t_3 = 14~\text{cm}.$
Selanjutnya, akan dicari panjang jari-jari kerucut sedang dan kecil
dengan menggunakan konsep kesebangunan.
Mencari nilai $r_2$:
$$\begin{aligned} \dfrac{r_1}{r_2} = \dfrac{t_1}{t_2} \Rightarrow
\dfrac{18}{r_2} & = \dfrac{42}{28} \\ \dfrac{18}{r_2} & =
\dfrac{3}{2} \\ r_2 & = 12~\text{cm} \end{aligned}$$Mencari
nilai $r_3$:
$$\begin{aligned} \dfrac{r_1}{r_3} = \dfrac{t_1}{t_3} \Rightarrow
\dfrac{18}{r_3} & = \dfrac{42}{14} \\ \dfrac{18}{r_3} & = 3
\\ r_3 & = 6~\text{cm} \end{aligned}$$Perbandingan volume
kerucut besar, sedang, dan kecil dinyatakan sebagai berikut.
$$\begin{aligned} V_{\text{besar}} : V_{\text{sedang}} :
V_{\text{kecil}} & = \color{blue}{\dfrac13} \pi r_1^2 t_1 :
\color{blue}{\dfrac13} \pi r_2^2 t_2 : \color{blue}{\dfrac13} \pi
r_3^2 t_3 \\ & = r_1^2 t_1 : r_2^2 t_2 : r_3^2 t_3 \\ & =
(18)^2(42) : \left(12\right)^2 (28) : \left(6\right)^2 (14) \\ &
= 9(3) : 4(2) : 1(1) \\ & = 27 : 8 : 1 \end{aligned}$$Jawaban
b)
Misalkan panjang garis pelukis kerucut besar, sedang, dan kecil
berturut-turut adalah $s_1, s_2$, dan $s_3$ sehingga
$$\begin{aligned} x & = s_2-s_3 \\ & = \sqrt{r_2^2 +
t_2^2}-\sqrt{r_3^2+t_3^2} \\ & = \sqrt{12^2 + 28^2}-\sqrt{6^2 +
14^2} \\ & = 4\sqrt{58}-2\sqrt{58} \\ & = 2\sqrt{58}
\end{aligned}$$dan
$$\begin{aligned} y & = s_1-s_2 \\ & = \sqrt{r_1^2 +
t_1^2}-\sqrt{r_2^2+t_2^2} \\ & = \sqrt{18^2 + 42^2}-\sqrt{12^2 +
28^2} \\ & = 6\sqrt{58}-4\sqrt{58} \\ & = 2\sqrt{58}
\end{aligned}$$Jadi, nilai $\boxed{x = y = 2\sqrt{58}}$
Soal Nomor 9
Sebuah tabung dimasukkan setengah bola dan di dalam setengah bola
dimasukkan lagi sebuah kerucut seperti tampak pada gambar.
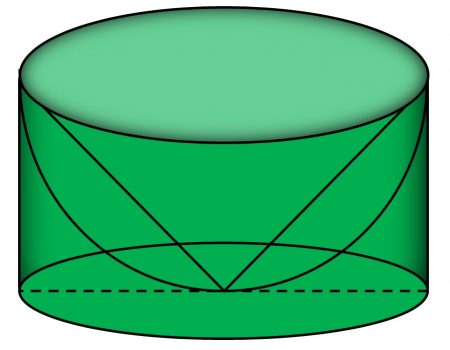
Tentukan rasio volume tabung, setengah bola, dan kerucut tersebut.
Pembahasan :
Misalkan tinggi kerucut besar, sedang, dan kecil berturut-turut
adalah $t_1, t_2$, dan $t_3$ sehingga $t_1 = 42~\text{cm}$, $t_2 =
28~\text{cm}$, dan $t_3 = 14~\text{cm}.$
Selanjutnya, akan dicari panjang jari-jari kerucut sedang dan kecil
dengan menggunakan konsep kesebangunan.
Mencari nilai $r_2$:
$$\begin{aligned} \dfrac{r_1}{r_2} = \dfrac{t_1}{t_2} \Rightarrow
\dfrac{18}{r_2} & = \dfrac{42}{28} \\ \dfrac{18}{r_2} & =
\dfrac{3}{2} \\ r_2 & = 12~\text{cm} \end{aligned}$$Mencari
nilai $r_3$:
$$\begin{aligned} \dfrac{r_1}{r_3} = \dfrac{t_1}{t_3} \Rightarrow
\dfrac{18}{r_3} & = \dfrac{42}{14} \\ \dfrac{18}{r_3} & = 3
\\ r_3 & = 6~\text{cm} \end{aligned}$$Perbandingan volume
kerucut besar, sedang, dan kecil dinyatakan sebagai berikut.
$$\begin{aligned} V_{\text{besar}} : V_{\text{sedang}} :
V_{\text{kecil}} & = \color{blue}{\dfrac13} \pi r_1^2 t_1 :
\color{blue}{\dfrac13} \pi r_2^2 t_2 : \color{blue}{\dfrac13} \pi
r_3^2 t_3 \\ & = r_1^2 t_1 : r_2^2 t_2 : r_3^2 t_3 \\ & =
(18)^2(42) : \left(12\right)^2 (28) : \left(6\right)^2 (14) \\ &
= 9(3) : 4(2) : 1(1) \\ & = 27 : 8 : 1 \end{aligned}$$Jawaban
b)
Misalkan panjang garis pelukis kerucut besar, sedang, dan kecil
berturut-turut adalah $s_1, s_2$, dan $s_3$ sehingga
$$\begin{aligned} x & = s_2-s_3 \\ & = \sqrt{r_2^2 +
t_2^2}-\sqrt{r_3^2+t_3^2} \\ & = \sqrt{12^2 + 28^2}-\sqrt{6^2 +
14^2} \\ & = 4\sqrt{58}-2\sqrt{58} \\ & = 2\sqrt{58}
\end{aligned}$$dan
$$\begin{aligned} y & = s_1-s_2 \\ & = \sqrt{r_1^2 +
t_1^2}-\sqrt{r_2^2+t_2^2} \\ & = \sqrt{18^2 + 42^2}-\sqrt{12^2 +
28^2} \\ & = 6\sqrt{58}-4\sqrt{58} \\ & = 2\sqrt{58}
\end{aligned}$$Jadi, nilai $\boxed{x = y = 2\sqrt{58}}$
Soal Nomor 9
Sebuah tabung dimasukkan setengah bola dan di dalam setengah bola
dimasukkan lagi sebuah kerucut seperti tampak pada gambar.

Tentukan rasio volume tabung, setengah bola, dan kerucut tersebut.
Pembahasan :
Dari gambar, tampak bahwa panjang jari-jari alas tabung,
alas
kerucut, dan setengah bola itu sama, yaitu $r$. Tinggi tabung dan
tinggi kerucut juga sama dengan panjang jari-jari bola, yaitu $t =
r$.
Kita peroleh
$$\begin{aligned} & V_{\text{tabung}} : V_{\text{1/2 bola}} :
V_{\text{kerucut}} \\ & = \pi r^2 t : \dfrac12 \cdot \dfrac43\pi
r^3 : \dfrac13 \pi r^2 t \\ & = \pi r^2 (r) : \dfrac12 \cdot
\dfrac43\pi r^3 : \dfrac13 \pi r^2 (r) \\ & = \color{red}{\pi
r^3} : \dfrac23 (\color{red}{\pi r^3}) : \dfrac13 (\color{red}{\pi
r^3}) \\ & = 1 : \dfrac23 : \dfrac13 \\ & = 3 : 2 : 1
&& (\text{Dikali 3}) \end{aligned}$$Jadi, rasio volume
tabung, setengah bola, dan kerucut tersebut adalah $\boxed{3 : 2 :
1}$
Soal Nomor 10
Hitunglah volume bola terbesar yang dapat dimasukkan ke dalam kotak
yang berukuran $70~\text{cm} \times 20~\text{cm} \times 58~\text{cm}$,
dengan asumsi $\pi = 3,14.$
Pembahasan :
kerucut, dan setengah bola itu sama, yaitu $r$. Tinggi tabung dan
tinggi kerucut juga sama dengan panjang jari-jari bola, yaitu $t =
r$.
Kita peroleh
$$\begin{aligned} & V_{\text{tabung}} : V_{\text{1/2 bola}} :
V_{\text{kerucut}} \\ & = \pi r^2 t : \dfrac12 \cdot \dfrac43\pi
r^3 : \dfrac13 \pi r^2 t \\ & = \pi r^2 (r) : \dfrac12 \cdot
\dfrac43\pi r^3 : \dfrac13 \pi r^2 (r) \\ & = \color{red}{\pi
r^3} : \dfrac23 (\color{red}{\pi r^3}) : \dfrac13 (\color{red}{\pi
r^3}) \\ & = 1 : \dfrac23 : \dfrac13 \\ & = 3 : 2 : 1
&& (\text{Dikali 3}) \end{aligned}$$Jadi, rasio volume
tabung, setengah bola, dan kerucut tersebut adalah $\boxed{3 : 2 :
1}$
Soal Nomor 10
Hitunglah volume bola terbesar yang dapat dimasukkan ke dalam kotak
yang berukuran $70~\text{cm} \times 20~\text{cm} \times 58~\text{cm}$,
dengan asumsi $\pi = 3,14.$
Pembahasan :
Bola terbesar yang dapat dimasukkan ke dalam kotak tersebut
berdiameter $d = 20~\text{cm}$ sehingga $r = 10~\text{cm}$. Kita
peroleh
$$\begin{aligned} V & = \dfrac43 \pi r^3 \\ & = \dfrac43
\cdot 3,14 \cdot (10)^3 \\ & = \dfrac43 \cdot 314 =
\dfrac{1.256}{3} \end{aligned}$$Jadi, volume bola terbesar yang
dimaksud adalah $\boxed{\dfrac{1.256}{3}~\text{cm}^3}$
berdiameter $d = 20~\text{cm}$ sehingga $r = 10~\text{cm}$. Kita
peroleh
$$\begin{aligned} V & = \dfrac43 \pi r^3 \\ & = \dfrac43
\cdot 3,14 \cdot (10)^3 \\ & = \dfrac43 \cdot 314 =
\dfrac{1.256}{3} \end{aligned}$$Jadi, volume bola terbesar yang
dimaksud adalah $\boxed{\dfrac{1.256}{3}~\text{cm}^3}$
--- EoF---
🎯Terimakasih, anda telah membaca postingan dengan judul:
📚 "Bangun Ruang (Pra-Olimpiade) Soal dan Pembahasan", semoga postingan ini bermanfaat untuk anda."Matematika adalah bahasa yang digunakan alam untuk berbicara dengan kita." 😊- Galileo Galilei
