Materi SMP Tentang Peluang (Probabilitas) SMP |Soal-Soal dan Pembahasan|
Materi peluang yang diajarkan pada tingkat SMP meliputi konsep dasar
tentang peluang, ruang sampel, peristiwa, dan peluang suatu peristiwa.
Berikut adalah penjelasan singkat tentang materi-materi tersebut:
Konsep dasar tentang peluang: Peluang merupakan kemungkinan suatu
peristiwa terjadi. Peluang dinyatakan dalam bentuk pecahan atau desimal
dari 0 sampai 1.
Ruang sampel:
Ruang sampel adalah himpunan semua kemungkinan hasil dari
suatu eksperimen. Contohnya, jika kita melempar sebuah dadu enam sisi,
maka ruang sampelnya adalah {1, 2, 3, 4, 5, 6}.
Peristiwa:
Peristiwa adalah himpunan bagian dari ruang sampel. Contohnya,
jika kita ingin mencari peluang munculnya angka genap pada dadu, maka
peristiwa tersebut adalah {2, 4, 6}.
Peluang suatu peristiwa:
Peluang suatu peristiwa dinyatakan dengan
rumus $\begin{equation}{P}{\left({A} \right)}={\frac{{n}{\left({A} \right)}}{{n}{\left({S} \right)}}}\end{equation}$, di mana $P(A)$ adalah peluang peristiwa A
terjadi, $n(A)$ adalah banyaknya hasil yang memenuhi peristiwa A, dan $n(S)$ adalah banyaknya hasil pada ruang sampel.
Selain itu, di tingkat SMP juga diajarkan tentang cara menghitung peluang
gabungan, peluang komplementer, dan peluang acak. Peluang gabungan adalah
peluang terjadinya dua peristiwa atau lebih pada waktu yang sama. Peluang
komplementer adalah peluang terjadinya suatu peristiwa A tidak terjadi.
Sedangkan, peluang acak adalah peluang terjadinya suatu peristiwa tanpa
pengaruh dari peristiwa sebelumnya.
Dalam pembelajaran peluang di tingkat SMP, siswa biasanya diberikan
latihan soal dan permainan untuk mengasah kemampuan mereka dalam
menghitung peluang.
Berikut adalah beberapa contoh soal peluang untuk tingkat SMP beserta
penyelesaiannya:
Diberikan sebuah dadu enam sisi. Tentukan peluang munculnya angka
ganjil.
Penyelesaian: Ruang sampel pada lemparan dadu adalah {1, 2, 3,
4, 5, 6}. Peluang munculnya angka ganjil adalah 1/2, karena ada 3 angka
ganjil dari 6 kemungkinan hasil.
Diberikan sebuah kartu remi yang berisi 52 kartu. Tentukan peluang
munculnya kartu hati.
Penyelesaian: Ruang sampel pada kartu remi adalah 52 kartu.
Peluang munculnya kartu hati adalah 1/4, karena ada 13 kartu hati dari
52 kartu.
Diberikan sebuah kotak berisi 4 bola merah dan 6 bola hijau. Tentukan
peluang mengambil bola merah secara acak.
Penyelesaian: Ruang sampel pada kotak bola adalah 10 bola.
Peluang mengambil bola merah secara acak adalah 4/10 atau 2/5, karena
ada 4 bola merah dari 10 bola keseluruhan.
Diberikan dua dadu enam sisi. Tentukan peluang munculnya jumlah kedua
dadu tersebut adalah 7.
Penyelesaian: Ruang sampel pada dua dadu adalah 36 kemungkinan hasil.
Peluang munculnya jumlah 7 adalah 6/36 atau 1/6, karena ada 6
kemungkinan hasil yang menghasilkan jumlah 7.
Diberikan sebuah koin fair yang dilempar dua kali. Tentukan peluang
munculnya dua sisi yang sama.
Penyelesaian: Ruang sampel pada dua lemparan koin adalah 4 kemungkinan
hasil (HH, HT, TH, TT). Peluang munculnya dua sisi yang sama adalah 2/4
atau 1/2, karena ada 2 kemungkinan hasil yang menghasilkan dua sisi yang
sama (HH dan TT).
Berikut ini merupakan soal dan pembahasan mengenai peluang (probabilitas)
yang dianjurkan untuk dipelajari oleh siswa tingkat SMP/Sederajat,
terutama untuk menguatkan pemahaman konsep dan persiapan ulangan
semester.
Bagian Pilihan Ganda
Soal Nomor 1
Perhatikan beberapa kejadian/peristiwa berikut.
Munculnya mata dadu $7$ dari hasil pelemparan sebuah dadu.
Kelahiran seorang bayi laki-laki.
Terambilnya kartu bernomor $11$ dari satu set kartu remi.
Kematian seorang manusia.
Terbitnya matahari setiap harinya.
Munculnya api di kedalaman lautan.
Seekor kucing dapat berbahasa Indonesia.
Dari kejadian/peristiwa di atas, manakah yang memiliki peluang kejadian
$0$?
A. 1, 3, 6, dan 7
B. 2, 4, dan 5
C. 1, 5, dan 6
D. 3, 6, dan 7
Suatu kejadian memiliki peluang $0$ berarti kejadian tersebut tidak
mungkin terjadi.
Munculnya mata dadu $7$ dari hasil pelemparan sebuah dadu merupakan
kejadian yang tidak mungkin terjadi karena jumlah mata dadu tertinggi
pada dadu adalah $6$.
Kelahiran seorang bayi laki-laki adalah kejadian yang biasa/mungkin
terjadi.
Terambilnya kartu bernomor $11$ dari satu set kartu remi merupakan
kejadian yang tidak mungkin terjadi karena kartu remi hanya sampai
bernomor $10$.
Kematian merupakan kejadian yang pasti dialami oleh setiap manusia
(memiliki peluang $1$).
Terbitnya matahari setiap pagi merupakan kejadian yang pasti terjadi
(memiliki peluang $1$).
Munculnya api di kedalaman lautan merupakan hal yang mustahil karena
api tidak akan menyala di dalam air.
Seekor kucing dapat berbahasa Indonesia merupakan kejadian yang
mustahil.
Berdasarkan uraian di atas, dapat disimpulkan bahwa kejadian dengan
peluang $0$ adalah 1, 3, 6, dan 7.
(Jawaban A)
Soal Nomor 2
Dalam percobaan melambungkan $3$ mata uang logam, peluang muncul $2$ angka
$1$ gambar adalah $\cdots \cdot$
A. $\dfrac18$ C. $\dfrac23$
B. $\dfrac38$ D. $\dfrac58$
Misalkan $M$ adalah kejadian munculnya $2$ angka ($A$) $1$ gambar $(G),$
maka
$M = \{(A, A, G), (A, G, A), (G, A, A)\}$
dengan $n(M) = 3.$
Banyaknya anggota ruang sampel untuk $3$ koin yang masing-masingnya
memiliki $2$ sisi adalah $n(S) = 2 \times 2 \times 2 = 8.$
Jadi, peluangnya adalah $\boxed{p(M) = \dfrac{n(M)} {n(S)} =
\dfrac{3}{8}}$
(Jawaban B)
Soal Nomor 3
Dalam percobaan melempar undi $3$ koin uang logam secara bersamaan, peluang
muncul $1$ angka adalah $\cdots \cdot$
A. $\dfrac38$ C. $\dfrac35$
B. $\dfrac23$ D. $\dfrac58$
Misalkan $M$ adalah kejadian munculnya $1$ angka ($A$), yang berarti koin
lainnya muncul gambar ($G$) sehingga
$M = \{(A, G, G), (G, A, G), (G, G, A)\}$ dengan $n(M) = 3.$
Banyaknya anggota ruang sampel untuk $3$ koin yang masing-masingnya
memiliki $2$ sisi adalah $n(S) = 2 \times 2 \times 2 = 8.$
Jadi, peluangnya adalah $\boxed{p(M) = \dfrac{n(M)} {n(S)} =
\dfrac{3}{8}}$
(Jawaban A)
Soal Nomor 4
Pada pelemparan $3$ mata uang logam yang dilakukan dalam tempo waktu yang
sama sebanyak $80$ kali, frekuensi harapan munculnya paling sedikit $1$
angka dari pelemparan uang logam itu adalah ....
A. $70$ kali
B. $60$ kali
C. $50$ kali
D. $40$ kali
Misalkan $M$ adalah kejadian munculnya paling sedikit $1$ angka $(A)$
sehingga
$$\begin{aligned} & M = \{(A, G, G), (G, A, G), (G, G, A), \\ &
(A, A, G), (A, G, A), (G, A, A), (A, A, A)\} \end{aligned}$$dengan $G$
gambar dan $n(M) = 7.$
Banyaknya anggota ruang sampel untuk $3$ koin yang masing-masingnya
memiliki $2$ sisi adalah $n(S) = 2 \times 2 \times 2 = 8.$
Jadi, peluangnya adalah $p(M) = \dfrac{n(M)} {n(S)} = \dfrac{7}{8}.$
Frekuensi harapan munculnya paling sedikit $1$ angka dari pelemparan uang
logam itu adalah $\boxed{p(M) \times n = \dfrac{7}{8} \times 80 = 70~\text{kali}}$
(Jawaban A)
Soal Nomor 5
Dua buah dadu dilambungkan bersamaan. Peluang muncul mata dadu berjumlah
$4$ adalah $\cdots \cdot$
A. $\dfrac{1}{12}$
B. $\dfrac18$
C. $\dfrac16$
D. $\dfrac14$
Misalkan $A$ adalah kejadian munculnya jumlah mata dadu $4$
sehingga
$A = \{(1, 3), (3, 1), (2, 2)\}$ dengan $n(A) = 3.$
Banyaknya anggota ruang sampel untuk $2$ dadu yang masing-masingnya
memiliki $6$ sisi adalah $n(S) = 6 \times 6 \times = 36.$
Jadi, peluangnya adalah $\boxed{p(A) = \dfrac{n(A)} {n(S)} = \dfrac{3}{36}= \dfrac{1}{12}}$
(Jawaban A)
Soal Nomor 6
Dua buah dadu dilempar undi. Peluang muncul kedua mata dadu berjumlah lebih
dari $7$ adalah $\cdots \cdot$
A. $\dfrac{7}{12}$
B. $\dfrac{5}{12}$
C. $\dfrac{5}{18}$
D. $\dfrac16$
Berjumlah lebih dari $7$, berarti boleh $8, 9, 10, 11$, atau $12$.
Misalkan $A$ adalah kejadian munculnya jumlah mata dadu $8$
sehingga
$A = \{(2, 6), (6, 2), (3, 5), (5, 3), (4, 4)\}$
dengan $n(A) = 5.$
Misalkan $B$ adalah kejadian munculnya jumlah mata dadu $9$ sehingga
$B = \{(3, 6), (6, 3), (4, 5), (5, 4)\}$
dengan $n(B) = 4.$
Misalkan $C$ adalah kejadian munculnya jumlah mata dadu $10$
sehingga
$C = \{(4, 6), (6, 4), (5, 5)\}$
dengan $n(C) = 3.$
Misalkan $D$ adalah kejadian munculnya jumlah mata dadu $11$
sehingga
$D = \{(5, 6), (6, 5)\}$
dengan $n(D) = 2.$
Misalkan $E$ adalah kejadian munculnya jumlah mata dadu $12$
sehingga
$E = \{(6, 6)\}$
dengan $n(E) = 1.$
Banyaknya anggota ruang sampel untuk $2$ dadu yang masing-masingnya
memiliki $6$ sisi adalah $n(S) = 6 \times 6 = 36.$
Jadi, peluangnya adalah
$$\begin{aligned} & p(A \cup B \cup C \cup D \cup E) \\ & =
\dfrac{n(A) + n(B) + n(C) + n(D) + n(E)} {n(S)} \\ & =
\dfrac{5+4+3+2+1}{36} \\ & = \dfrac{15}{36} = \dfrac{5}{12}
\end{aligned}$$(Jawaban B)
Soal Nomor 7
Dalam percobaan melempar undi dua buah dadu secara bersama-sama, peluang
muncul mata dadu berjumlah kurang dari $5$ adalah $\cdots \cdot$
A. $\dfrac16$ C. $\dfrac{5}{36}$
B. $\dfrac14$ D. $\dfrac{7}{18}$
Berjumlah kurang dari $5$, berarti boleh $2, 3$, atau $4.$
Misalkan $A$ adalah kejadian munculnya jumlah mata dadu $2$ sehingga $A = \{(1, 1)\}$ dengan $n(A) = 1.$
Misalkan $B$ adalah kejadian munculnya jumlah mata dadu $3$ sehingga
$B = \{(1, 2), (2, 1)\}$ dengan $n(B) = 2.$
Misalkan $C$ adalah kejadian munculnya jumlah mata dadu $4$
sehingga
$C = \{(1, 3), (3, 1), (2, 2)\}$ dengan $n(C) = 3.$
Banyaknya anggota ruang sampel untuk 2 dadu yang masing-masingnya
memiliki $6$ sisi adalah $n(S) = 6 \times 6 \times = 36.$
Jadi, peluangnya adalah
$$\begin{aligned} p(A \cup B \cup C) & = \dfrac{n(A) + n(B) + n(C)}
{n(S)} \\ & = \dfrac{1+2+3}{36} \\ & = \dfrac{6}{36} =
\dfrac{1}{6} \end{aligned}$$(Jawaban A)
Soal Nomor 8
Seorang pedagang telur memiliki $200$ butir telur. Karena kurang hati-hati,
$10$ butir telur pecah saat diletakkan di dalam peti. Jika sebutir telur
diambil secara acak, peluang terambilnya telur yang tidak pecah adalah
$\cdots \cdot$
A. $\dfrac{19}{20}$ C. $\dfrac{15}{20}$
B. $\dfrac{18}{20}$ D. $\dfrac{1}{20}$
Diketahui:
Jumlah telur seluruhnya = $200$
Jumlah telur yang pecah = $10$
Jumlah telur yang tidak pecah = $190.$
Peluang terambilnya telur yang tidak pecah adalah
$$\boxed{\dfrac{\text{Jumlah telur yang tidak pecah}} {\text{Jumlah telur
seluruhnya}} =\dfrac{190}{200} =\dfrac{19}{20}}$$(Jawaban A)
Soal Nomor 9
Sebuah kantong berisi $60$ kelereng identik terdiri dari $8$ kelereng
merah, $12$ kuning, $16$ hijau, dan sisanya biru. Jika diambil sebutir
kelereng secara acak, peluang terambilnya kelereng biru adalah $\cdots
\cdot$
A. $\dfrac{1}{24}$ C. $\dfrac25$
B. $\dfrac15$ D. $\dfrac12$
Misalkan $B$ menyatakan kejadian terambilnya kelereng biru dalam kantong
itu.
Banyaknya kelereng biru dalam kantong itu adalah
$n(B) = 60 -8 -12 -16 = 24.$
Banyaknya seluruh kelereng adalah $n(S) = 60.$
Jadi, peluang terambilnya sebutir kelereng biru adalah
$\boxed{p(B) = \dfrac{n(B)} {n(S)} = \dfrac{24}{60} = \dfrac25}$
(Jawaban C)
Soal Nomor 10
Dalam suatu kantong terdapat $30$ kelereng putih, $18$ kelereng biru, dan
$32$ kelereng merah. Jika dari dalam kantong tersebut diambil satu kelereng
secara acak, peluang terambil kelereng merah adalah $\cdots \cdot$
A. $0,32$ C. $0,60$
B. $0,40$ D. $0,80$
Misalkan $M$ menyatakan kejadian terambilnya kelereng merah dalam kantong
itu.
Banyaknya kelereng merah dalam kantong itu adalah $n(M) = 32.$
Banyaknya seluruh kelereng adalah
$n(S) = 30 + 18 + 32 = 80.$
Jadi, peluang terambilnya sebutir kelereng merah adalah
$\boxed{p(M) = \dfrac{n(M)} {n(S)} = \dfrac{32}{80} = \dfrac{4}{10} =
0,40}$
(Jawaban B)
Soal Nomor 11
Sebuah kubus mempunyai $2$ sisi berwarna merah, $2$ sisi berwarna kuning,
$1$ sisi berwarna hijau, dan $1$ sisi berwarna biru. Kubus itu dilempar
undi. Peluang muncul sisi bagian atas berwarna merah adalah $\cdots
\cdot$
A. $\dfrac23$ C. $\dfrac13$
B. $\dfrac12$ D. $\dfrac16$
Banyaknya sisi berwarna merah ada $2.$
Banyaknya sisi kubus ada $6$.
Peluang muncul sisi bagian atas berwarna merah adalah $\boxed{\dfrac26 =
\dfrac13}$
(Jawaban C)
Soal Nomor 12
Dari $180$ orang yang hadir dalam suatu acara disediakan $9$ hadiah untuk
doorprize. Peluang yang hadir akan mendapatkan hadiah
doorprize
adalah $\cdots \cdot$
A. $0,50$ C. $0,05$
B. $0,20$ D. $0,02$
Misalkan $D$ menyatakan kejadian didapatnya doorprize.
Banyak doorprize yang disediakan adalah $n(D) = 9.$
Banyak orang yang hadir adalah $n(S) = 180.$
Jadi, peluang didapatnya doorprize adalah $\boxed{p(D) =
\dfrac{n(D)} {n(S)}= \dfrac{9}{180} = 0,05}$
(Jawaban C)
Soal Nomor 13
Sebuah dadu dilambungkan sebanyak $120$ kali. Frekuensi harapan munculnya
mata dadu bilangan prima adalah $\cdots \cdot$
A. $20$ kali C. $40$ kali
B. $30$ kali D. $60$ kali
Mata dadu yang mungkin muncul dalam pelambungan sebuah dadu adalah
$\{1,2,3,4,5,6\}$, dengan $2, 3, 5$ (ada sebanyak $3$) sebagai bilangan
prima.
Misalkan kejadian munculnya mata dadu prima dinotasikan dengan simbol
$A$.
Dengan demikian, peluang munculnya mata dadu prima adalah
$p(A) = \dfrac{3}{6} = \dfrac12.$
Frekuensi harapan munculnya mata dadu prima dari $n = 120$ kali
pelambungan adalah
$\begin{aligned} f_h & = p(A) \times n \\ & = \dfrac12 \times 120
= 60 \end{aligned}$
Jadi, frekuensi harapan munculnya mata dadu bilangan prima adalah
$\boxed{60~\text{kali}}$
(Jawaban D)
Soal Nomor 14
Sebuah huruf dipilih secara acak dari huruf-huruf pembentuk kata
“INDONESIA”. Peluang terpilihnya huruf N adalah $\cdots \cdot$
A. $\dfrac19$ C. $\dfrac39$
B. $\dfrac29$ D. $\dfrac49$
Huruf N muncul 2 kali dari kata INDONESIA. Kata tersebut terdiri dari 9
huruf. Untuk itu, peluang terpilihnya huruf N sebesar $\dfrac29$.
(Jawaban B)
Soal Nomor 15
Dari seperangkat kartu bridge, diambil sebuah kartu secara acak. Peluang
terambilnya kartu bernomor genap adalah $\cdots \cdot$
A. $\dfrac19$ C. $\dfrac{4}{13}$
B. $\dfrac{5}{52}$ D. $\dfrac{5}{13}$
Pada kartu bridge (remi), jumlah kartunya sebanyak $52$ lembar.
Kartu bernomor dimulai dari $1$ (kartu As) sampai $10$, masing-masingnya
terdiri dari $4$ seri, yaitu heart ♥, spade ♠, diamond ♦, dan club
♣.
Karena nomor genapnya ada $5$, yaitu $2, 4, 6, 8$, dan $10$, serta
masing-masingnya ada $4$ seri, maka jumlah kartu bernomor genap ada
sebanyak $4 \times 5 = 20.$
Misalkan kejadian munculnya kartu bernomor genap dinotasikan dengan $A$,
maka $\boxed{P(A) = \dfrac{20}{52} = \dfrac{5}{13}}$
(Jawaban D)
Soal Nomor 16
Seorang ibu ingin mempunyai $2$ orang anak. Kemungkinan kelahiran anak
laki-laki dan perempuan diasumsikan sama. Peluang kedua anaknya perempuan
adalah $\cdots \cdot$
A. $\dfrac14$ C. $\dfrac34$
B. $\dfrac12$ D. $1$
Peluang kelahiran anak laki-laki sama dengan peluang kelahiran anak
perempuan, yaitu $\dfrac12$.
Peluang kedua anaknya perempuan ($2$ kejadian) adalah
$\underbrace{\dfrac12}_{\text{perempuan}} \times
\underbrace{\dfrac12}_{\text{perempuan}} = \dfrac14.$
(Jawaban A)
Soal Nomor 17
Dalam kantong terdapat tiga bola berwarna merah diberi nomor $1 – 3$, lima
bola berwarna kuning diberi nomor $4 – 8$, dan empat bola berwarna hijau
diberi nomor $9 – 12$. Tiga bola diambil satu per satu secara acak dari
dalam kantong. Pengambilan pertama, muncul bola merah bernomor genap dan
tidak dikembalikan. Pengambilan kedua, muncul bola hijau bernomor prima dan
tidak dikembalikan. Peluang terambilnya bola bernomor ganjil pada
pengambilan ketiga adalah $\cdots \cdot$
A. $30\%$ C. $50\%$
B. $40\%$ D. $60\%$
Bola nomor $1, 2, 3$: merah.
Bola nomor $4, 5, 6, 7, 8$: kuning.
Bola nomor $9, 10, 11, 12$: hijau.
Pengambilan pertama muncul bola merah bernomor genap, artinya bola nomor
$2$ telah diambil.
Pengambilan kedua muncul bola hijau bernomor prima, artinya bola nomor
$11$ telah diambil.
Sisa bola bernomor ganjil: $1, 3, 5, 7, 9$ (ada $5$ bola).
Jumlah seluruh bola ada $12 -2 = 10.$
Jadi, peluang terambilnya bola bernomor ganjil pada pengambilan ketiga
adalah $\boxed{\dfrac{5}{10} = 50\%}$
(Jawaban C)
Soal Nomor 18
Sebuah kotak berisi $18$ bola yang terdiri dari warna merah, biru, dan
hijau. Bola merah diberi nomor $1$ sampai dengan $8$, bola biru diberi nomor
$9$ sampai dengan $14$, dan bola hijau diberi nomor $15$ sampai dengan $18$.
Tiga bola diambil acak secara berurutan satu per satu tanpa pengembalian.
Pengambilan bola pertama bernomor $7$ dan pengambilan bola kedua bernomor
$13$. Peluang pengambilan bola ketiga bernomor genap hijau adalah $\cdots
\cdot$
A. $\dfrac{2}{16}$ C. $\dfrac{7}{18}$
B. $\dfrac{4}{16}$ D. $\dfrac{7}{16}$
Bola nomor $1, 2, 3, 4, 5, 6, 7, 8$: merah.
Bola nomor $9, 10, 11, 12, 13, 14$: biru.
Bola nomor $15, 16, 17, 18$: hijau.
Pengambilan pertama muncul bola bernomor $7$.
Pengambilan kedua muncul bola bernomor $13$.
Sisa bola bernomor genap hijau: $16, 18$ (ada $2$ bola).
Jumlah seluruh bola ada $18 -2 = 16.$
Jadi, peluang terambilnya bola bernomor genap pada pengambilan ketiga
adalah $\boxed{\dfrac{2}{16}}$
(Jawaban A)
Soal Nomor 19
Dilla diperbolehkan ibunya untuk mengambil satu permen dari sebuah kantong.
Dia tidak dapat melihat warna permen tersebut. Banyaknya permen dengan
masing-masing warna dalam kantong tersebut ditunjukkan dalam grafik
berikut.
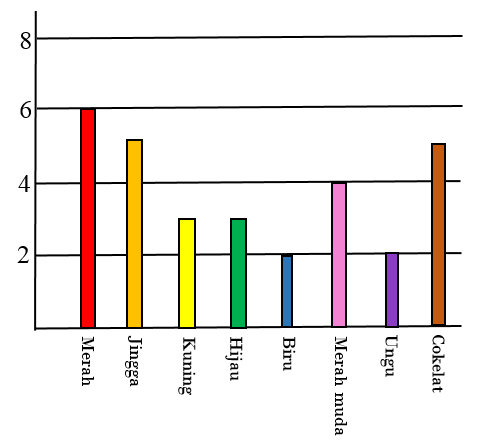
Berapakah peluang Dilla mengambil sebutir permen warna merah?
A. $10\%$ C. $25\%$
B. $20\%$ D. $50\%$
Jumlah permen warna merah ada $6$ butir.
Jumlah permen seluruhnya ada $6 + 5 + 3 + 3 + 2 + 4 + 2 + 5 = 30$
butir.
Jadi, peluang Dilla mengambil sebutir permen warna merah adalah
$\boxed{\dfrac{6}{30} = \dfrac{1}{5} = 20\%}$
(Jawaban B)
Soal Nomor 20
Dalam kantong terdapat $40$ permen dengan warna dan kuantitas seperti
tampak pada diagram lingkaran di bawah.
Flove mengambil sebutir permen dari kantong tanpa melihat warnanya. Peluang
Flove mengambil permen berwarna merah adalah $\cdots \cdot$
A. $54\%$ C. $10\%$
B. $15\%$ D. $5\%$
Kuantitas (jumlah) permen warna merah dalam satuan derajat adalah
$$\begin{aligned} & 360^{\circ} -(18+36+108+36+18+90)^{\circ} \\
& = 360^{\circ} -306^{\circ} = 54^{\circ} \end{aligned}$$Banyaknya
permen warna merah dalam kantong itu adalah
$\text{n}(\text{merah}) = \dfrac{54^{\circ}} {\cancelto{9}{360}^{\circ}}
\times \cancel{40} = 6.$
Peluang terambilnya sebutir permen warna merah adalah
$p(\text{merah}) = \dfrac{\text{n(merah)}} {\text{n} (S)} = \dfrac{6}{40}
= 15\%.$
(Jawaban B)
Soal Nomor 21
Di suatu kelas akan dipilih seorang ketua kelas dan wakil ketua kelas.
Kelas tersebut terdiri dari $16$ siswa laki-laki dan $24$ siswa perempuan.
Peluang terpilihnya ketua kelas perempuan dan wakil ketua kelas laki-laki
adalah $\cdots \cdot$
A. $\dfrac{13}{65}$ C. $\dfrac{16}{65}$
B. $\dfrac{14}{65}$ D. $\dfrac{19}{65}$
Misalkan $A$ kejadian terpilihnya ketua kelas perempuan, dengan $n(A) =
24$ dan $n(S) = 40$ sehingga $p(A) = \dfrac{n(A)} {n(S)} = \dfrac{24}{40} = \dfrac35.$
Misalkan $B$ kejadian terpilihnya wakil ketua kelas laki-laku, dengan
$n(B) = 16$ dan $n(S) = 40 -1 = 39$ (dikurangi $1$ karena sebelumnya sudah
dipilih satu orang perempuan menjadi ketua kelas) sehingga $p(B) = \dfrac{n(B)} {n(S)} = \dfrac{16}{39}.$
Dengan demikian, peluang terpilihnya ketua kelas perempuan dan wakil
ketua kelas laki-laki adalah
$\boxed{\begin{aligned} p(A \cap B) & = \dfrac{n(A)} {n(S)} \times
\dfrac{n(B)} {n(S)} \\ & = \dfrac{3}{5} \times \dfrac{16}{39} =
\dfrac{16}{65} \end{aligned}}$
(Jawaban C)
Soal Nomor 22
Dilan dan Milea berbelanja di toko yang sama dalam minggu yang sama selama
$5$ hari (Senin sampai Jumat). Mereka masing-masing memiliki peluang yang
sama untuk berbelanja di toko pada $5$ hari tersebut. Peluang mereka
berbelanja di toko itu pada hari yang berurutan adalah ....
A. $0,20$ C. $0,32$
B. $0,25$ D. $0,50$
Perhatikan tabel berikut.
Sel tabel yang diberi warna biru menyatakan kejadian di mana mereka
berdua berbelanja di hari yang berurutan. Dari tabel di atas, terdapat $8$
sel biru, sedangkan jumlah sel seluruhnya ada $25$. Jadi, peluangnya
sebesar $\boxed{\dfrac{8}{25} = 0,32}$
(Jawaban C)
Soal Nomor 23
Dalam suatu kantong terdapat $8$ bola bernomor $1$ sampai dengan $8$. Jika
diambil dua bola sekaligus, maka peluang terambil dua bola bernomor
berurutan adalah $\cdots \cdot$
A. $\dfrac17$ C. $\dfrac15$
B. $\dfrac16$ D. $\dfrac14$
Perhatikan tabel berikut.
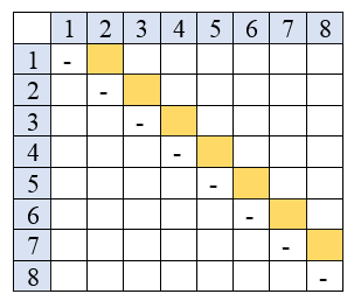
Pasangan dua bilangan yang berurutan adalah
$$(1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7), (7, 8).$$atau
sebaliknya. Karena dua bola diambil sekaligus, maka $(1, 2)$ dianggap sama
dengan $(2, 1)$. Jadi, hanya ada $7$ kemungkinan.
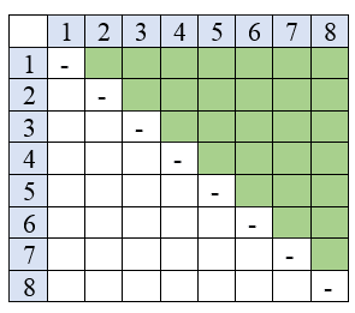
Banyak anggota ruang sampel seluruhnya ada $7 + 6 + 5 + 4 + 3 + 2 + 1 =
28$ (jumlah sel berwarna hijau pada tabel di atas).
Jadi, peluang terambil dua bola bernomor berurutan adalah
$\boxed{\dfrac{7}{28} = \dfrac14}$
(Jawaban D)
Soal Nomor 24
Sebuah kotak berisi $12$ bola bernomor $1$ sampai $12$. Jika diambil dua
bola sekaligus secara acak, peluang terambilnya $2$ bola bernomor ganjil
adalah $\cdots \cdot$
A. $\dfrac{30}{66}$ C. $\dfrac{15}{66}$
B. $\dfrac{45}{132}$ D. $\dfrac{15}{132}$
Alternatif 1: Perhatikan tabel berikut.
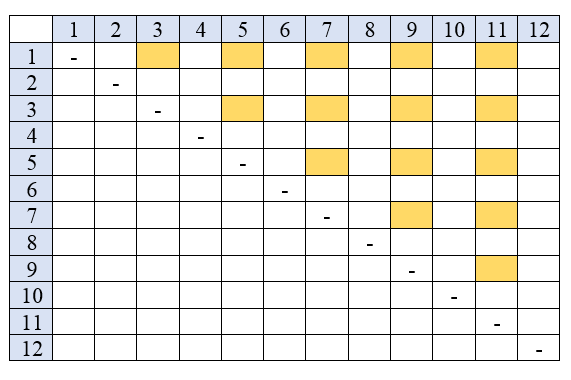Pasangan dua bilangan yang bernomor ganjil ditandai oleh sel berwarnajingga pada tabel di atas, yaitu sebanyak $5 + 4 + 3 + 2 + 1 = 15.$
Karena dua bola diambil sekaligus, maka $(1, 3)$ dianggap sama dengan
$(3, 1)$.
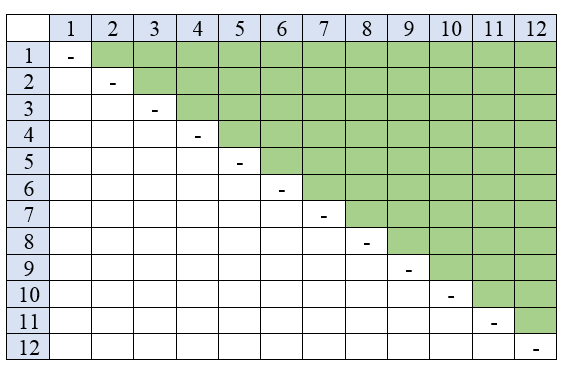Banyak anggota ruang sampel seluruhnya ada$\begin{aligned} 11 + 10 + & 9 + 8 + 7 + 6 + 5 + 4 +\\ & 3 + 2 + 1
= 66 \end{aligned}$
(jumlah sel berwarna hijau pada tabel di atas).
Jadi, peluang terambil dua bola bernomor berurutan adalah
$\boxed{\dfrac{15}{66}}$
Alternatif 2:
Dari bilangan $1$ sampai $12$, terdapat $6$ bilangan ganjil. Peluang
terambilnya satu bilangan ganjil dari kedua belas bilangan itu adalah
$P(A) = \dfrac{6}{12}$. Peluang terambil bilangan ganjil lagi dari sebelas
bilangan tersisa adalah $P(B) = \dfrac{5}{11}.$ Dengan demikian,
diperoleh
$P(A \cap B) = \dfrac{6}{12} \times \dfrac{5}{11} = \dfrac{30}{132} =
\dfrac{15}{66}.$
(Jawaban C)
Soal Nomor 25
Gambar di bawah merupakan sebuah roda putar yang dibagi menjadi $24$
bagian.
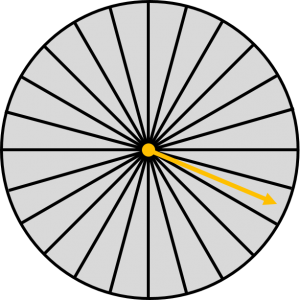Pada sebuah acara, seorang tamu memutar panah yang dapat berhenti di
sembarang bagian roda. Apabila terdapat $\dfrac{7}{24}$ bagian berwarna
biru, $\dfrac18$ bagian ungu, $\dfrac{5}{12}$ bagian kuning, dan sisanya
berwarna merah, maka warna yang paling sulit didapatkan (ditunjuk oleh
panah) adalah $\cdots \cdot$
A. biru C. kuning
B. ungu D. merah
Ubah tiap pecahan menjadi berpenyebut $24$.
Bagian berwarna biru ada sebanyak $\dfrac{7}{24}$.
Bagian berwarna ungu ada sebanyak $\dfrac18 = \dfrac{3}{24}$.
Bagian berwarna kuning ada sebanyak $\dfrac{5}{12} =
\dfrac{10}{24}$.
Bagian berwarna merah merupakan sisanya, yaitu $\dfrac{24-7-3-5}{24} =
\dfrac{9}{24}$.
Dari sini, diketahui bahwa ungu merupakan warna yang paling sulit didapat
karena bagiannya paling sedikit, yaitu $3$ dari $24$ bagian secara
keseluruhan. Dengan kata lain, peluang ditunjuknya warna ungu oleh panah
adalah yang paling kecil.
(Jawaban B)
Soal Nomor 26
Pada pelemparan sebuah dadu tak setimbang, peluang muncul mata dadu $1$
adalah $\dfrac15$ dari mata dadu yang lain. Peluang munculnya mata dadu
berjumlah genap pada pelemparan dadu itu adalah $\cdots \cdot$
A. $\dfrac{1}{10}$ D. $\dfrac{1}{6}$
B. $\dfrac{3}{20}$ E. $\dfrac{7}{20}$
C. $\dfrac{15}{26}$
Misalkan peluang munculnya mata dadu selain $1$ masing-masing adalah $x$
sehingga peluang munculnya mata dadu $1$ adalah $\dfrac15x.$ Karena jumlah
peluang setiap kejadian adalah $1,$ maka kita peroleh
$$\begin{aligned} \dfrac15x + x + x + x + x + x & = 1 \\
\dfrac{26}{5}x & = 1 \\ x & = \dfrac{5}{26} \end{aligned}$$Peluang
muncul mata dadu berjumlah genap $(2, 4, 6)$ diberikan oleh
$$\begin{aligned} P(\text{genap}) & = \dfrac{5}{26}+
\dfrac{5}{26}+\dfrac{5}{26} \\ & = \dfrac{15}{26}
\end{aligned}$$(Jawaban C)
Bagian Soal Uraian
Soal Nomor 1
Dari sekelompok anak, $25$ anak gemar matematika, $20$ anak gemar fisika,
dan $15$ anak gemar kedua-duanya. Jika setiap anak mempunyai peluang yang
sama untuk dipanggil, maka tentukan peluang dipanggilnya:
a. anak yang gemar kedua-duanya;
b. anak yang hanya gemar matematika.
Jumlah anak yang hanya gemar matematika adalah $n(M) = 25-15 = 10.$
Jumlah anak yang hanya gemar fisika adalah $n(M) = 20-15 = 5.$
Jumlah seluruh anak di kelompok itu adalah $$n(S) = (25-15)+(20-15)+15 = 30.$$Jawaban a)
Jumlah anak yang menggemari keduanya adalah $15$ orang. Peluang
dipanggilnya mereka sebesar $\dfrac{15}{30} = \dfrac12.$
Jawaban b)
Jumlah anak yang hanya gemar matematika adalah $n(M) = 25-15 = 10.$
Peluang dipanggilnya anak yang hanya gemar matematika adalah
$\dfrac{10}{30} = \dfrac13.$
Soal Nomor 2
Dua buah dadu dilempar bersama-sama. Jika $A$ merupakan kejadian
munculnya angka $4$ pada dadu pertama dan $B$ adalah kejadian munculnya
angka $4$ pada dadu kedua, apakah kejadian $A$ dan $B$ merupakan kejadian
saling bebas (independen)? Jelaskan.
Dua kejadian dikatakan saling bebas apabila kejadian yang satu tidak
memengaruhi kemungkinan terjadinya kejadian yang lain. Saat kita
melempar dua buah dadu, muncul atau tidaknya angka $4$ pada dadu pertama
tidak memengaruhi kemungkinan kemunculan angka $4$ pada dadu kedua.
Dalam hal ini, peluang kemunculan angka $4$ pada kedua dadu sama dengan
hasil kali peluang kemunculan angka $4$ pada masing-masing dadu, yaitu
$P(A \cap B) = P(A) \times P(B)$.
Dapat disimpulkan bahwa $A$ dan $B$ merupakan
kejadian saling bebas (independen).
Soal Nomor 3
Dari seperangkat kartu bridge dilakukan pengembalian secara acak sebanyak
$260$ kali. Setiap kali pengambilan, kartu dikembalikan. Berapa frekuensi
harapan yang diambil adalah kartu K?
Jumlah kartu bridge adalah $52$ lembar, sedangkan kartu K terdiri dari
4 lembar, yaitu K spade ♠, K heart ♥, K diamond ♦, dan K club ♣. Untuk
itu, peluang terambilnya selembar kartu K dari $52$ kartu tersebut
adalah $\color{blue}{\dfrac{4}{52} = \dfrac{1}{13}}.$
Frekuensi harapan terambilnya kartu K dari $\color{red}{260}$ kali
pengambilan adalah
$f_h = \color{blue}{\dfrac{1}{13}} \times \color{red}{260} = 20.$
Ini artinya dari $260$ kali pengambilan, diharapkan kita mendapatkan
$20$ kali kartu K.
Soal Nomor 4
Sembilan dari $10$ peluncuran roket dinyatakan sukses. Jika dalam tahun
ini akan dilakukan $50$ kali peluncuran roket, berapa roket yang
diharapkan sukses meluncur?
Peluang kesuksesan peluncuran roket adalah $\dfrac{9}{10}.$
Karena terdapat $50$ kali peluncuran roket, maka roket yang diharapkan
sukses meluncur adalah $\dfrac{9}{\cancel{10}} \times \cancelto{5}{50} =
45$ unit.
Soal Nomor 5
Misalkan kita melambungkan sekeping koin dan memutar sebuah spinner yang
memiliki tiga warna: merah, hijau, dan biru, secara sekaligus.
Apa ruang sampel dari hasil pelambungan koin?
Apa ruang sampel dari hasil pemutaran spinner?
Berapakah peluang kejadian muncul angka pada koin dan jarum spinner
menunjuk warna biru?
Gambarkan diagram yang dapat membantu kita untuk menentukan ruang
sampel dari pelambungan koin dan pemutaran spinner tersebut.
Jawaban a)
Ruang sampel dari pelambungan sekeping koin (memiliki $2$ sisi: angka
dan gambar) adalah $\{A, G\}$.
Jawaban b)
Ruang sampel dari hasil pemutaran spinner (memiliki $3$ warna: merah,
hijau, dan biru) adalah $\{\text{merah}, \text{hijau},
\text{biru}\}$.
Jawaban c)
Peluang kemunculan angka pada pelambungan koin adalah $\dfrac12.$
Peluang ditunjuknya warna biru oleh jarum spinner adalah
$\dfrac13.$
Dengan demikian, peluang kedua kejadian tersebut terjadi adalah
$P(A) = \dfrac12 \times \dfrac13 = \dfrac16.$
Jawaban d)
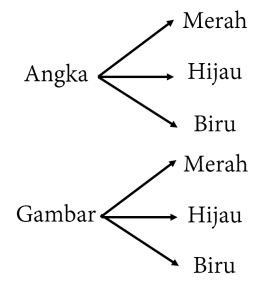
Soal Nomor 6
Jill sedang bermain kartu bersama temannya. Satu set kartu tersebut
terdiri dari $20$ kartu yang telah diberi nomor $1$ sampai $20$. Ketika
Jill mengambil sebuah kartu, tentukan peluang terambilnya:
kartu bernomor bilangan kuadrat;
kartu bernomor bilangan kubik;
kartu bernomor kurang dari $10$ dan genap;
kartu bernomor lebih dari $14$ dan ganjil.
Diketahui $\text{n}(S) = 20$.
Jawaban a)
Bilangan kuadrat adalah bilangan hasil pangkat dua.
Diketahui $A = \{1, 4, 9, 16\}$ sehingga $\text{n}(A) = 4$.
Peluang terambilnya kartu bernomor bilangan kuadrat adalah
$P(A) = \dfrac{\text{n}(A)}{\text{n}(S)} = \dfrac{4}{20} =
\dfrac15$.
Jawaban b)
Bilangan kubik dalah bilangan hasil pangkat tiga.
Diketahui $B = \{1, 8\}$ sehingga $\text{n}(B) = 2$.
Peluang terambilnya kartu bernomor bilangan kuadrat adalah
$P(B) = \dfrac{\text{n}(B)}{\text{n}(S)} = \dfrac{2}{20} =
\dfrac{1}{10}$.
Jawaban c)
Kartu yang dipilih bernomor kurang dari $10$ dan genap.
Diketahui $C = \{2, 4, 6, 8\}$ sehingga $\text{n}(C) = 4$.
Peluang terambilnya kartu bernomor bilangan kuadrat adalah
$P(C) = \dfrac{\text{n}(C)}{\text{n}(S)} = \dfrac{4}{20} =
\dfrac15$.
Jawaban d)
Kartu yang dipilih bernomor lebih dari $14$ dan ganjil.
Diketahui $D = \{15, 17, 19\}$ sehingga $\text{n}(D) = 3.$
Peluang terambilnya kartu bernomor bilangan kuadrat adalah
$P(D) = \dfrac{\text{n}(D)}{\text{n}(S)} = \dfrac{3}{20}.$
Soal Nomor 7
Seorang pesulap memainkan kartu remi yang melibatkan pengambilan sebuah
kartu dari satu set kartu remi tersebut. Tentukan peluang
terambilnya:
a. kartu Queen;
b. kartu bernomor $8$ atau $9$;
c. kartu bernomor genap;
d. kartu bernomor $7$ atau $♠$.
Jumlah kartu dalam satu set kartu remi adalah $\text{n}(S) = 52$.
Jawaban a)
Banyaknya kartu Queen adalah $\text{n}(\text{Q}) = 4$.
Peluang terambilnya kartu Queen adalah
$P(\text{Q}) = \dfrac{\text{n}(\text{Q})}{\text{n}(S)} = \dfrac{4}{52}
= \dfrac{1}{13}$.
Jawaban b)
Banyaknya kartu bernomor $8$ atau $9$ adalah $\text{n}(8~\text{atau}~9)
= 4+4 = 8$.
Peluang terambilnya kartu bernomor $8$ atau $9$ adalah
$$\begin{aligned} P(8~\text{atau}~9) & =
\dfrac{\text{n}(8~\text{atau}~9)}{\text{n}(S)} \\ & = \dfrac{8}{52}
= \dfrac{2}{13} \end{aligned}$$Jawaban c)
Banyaknya kartu bernomor genap $(2, 4, 6, 8, 10)$ adalah
$\text{n}(\text{genap}) = 5 \times 4 = 20.$
Peluang terambilnya kartu bernomor genal adalah
$P(\text{genap}) = \dfrac{\text{n}(\text{genap})}{\text{n}(S)} =
\dfrac{20}{52} = \dfrac{5}{13}.$
Jawaban d)
Banyaknya kartu bernomor $7$ adalah $\text{n}(7) = 4$.
Banyaknya kartu bergambar $♠$ adalah $\text{n}(♠) = 1 \times 13 =
13$.
Perhatikan bahwa ada $1$ kartu bernomor $7$ sekaligus $♠$ sehingga
$\text{n}(7~\text{atau spade}) = 4+13-1 = 16$.
Peluang terambilnya kartu bernomor genal adalah
$\begin{aligned} P(7~\text{atau}~♠) & =
\dfrac{\text{n}(7~\text{atau}~♠)}{\text{n}(S)} \\ & = \dfrac{16}{52}
= \dfrac{4}{13} \end{aligned}$
Soal Nomor 8
Seorang siswa mengambil dua kartu secara acak dari satu set kartu remi.
Tentukan peluang terambilnya bukan kartu berwajah (Jack, Queen, King) pada
pengambilan pertama dan kartu berwajah pada pengambilan kedua
apabila:
kartu dikembalikan pada pengambilan pertama;
kartu tidak dikembalikan pada pengambilan pertama.
Jawaban a)
Banyak kartu seluruhnya = $52$.
Banyak kartu berwajah = $4 \times 3 = 12.$
Peluang terambilnya bukan kartu berwajah (Jack, Queen, King) pada
pengambilan pertama adalah
$P(A) = \dfrac{52-12}{52} = \dfrac{40}{52} = \dfrac{10}{13}.$
Kartu dikembalikan sehingga jumlah kartu yang ada tetap $52$.
Peluang kartu berwajah pada pengambilan kedua adalah
$P(B) = \dfrac{12}{52} = \dfrac{3}{13}.$
Jadi, peluang dua kejadian tersebut terjadi adalah
$\begin{aligned} P(A \cap B) & = P(A) \times P(B) \\ & =
\dfrac{10}{13} \times \dfrac{3}{13} = \dfrac{30}{169}
\end{aligned}$
Jawaban b)
Banyak kartu seluruhnya = $52$.
Banyak kartu berwajah = $4 \times 3 = 12.$
Peluang terambilnya bukan kartu berwajah (Jack, Queen, King) pada
pengambilan pertama adalah
$P(A) = \dfrac{52-12}{52} = \dfrac{40}{52} = \dfrac{10}{13}.$
Kartu tidak dikembalikan sehingga jumlah kartu yang ada menjadi $51$ di
mana $1$ kartu tidak berwajah telah diambil.
Peluang kartu berwajah pada pengambilan kedua adalah
$P(B) = \dfrac{12}{51} = \dfrac{4}{17}.$
Jadi, peluang dua kejadian tersebut terjadi adalah
$\begin{aligned} P(A \cap B) & = P(A) \times P(B) \\ & =
\dfrac{10}{13} \times \dfrac{4}{17} = \dfrac{40}{221}
\end{aligned}$
Soal Nomor 9
Survei yang dilakukan terhadap $1108$ karyawan dari suatu perusahaan
menunjukkan bahwa sebanyak $621$ karyawan menggunakan bus untuk pergi
bekerja, $445$ karyawan menggunakan kereta. Diketahui juga bahwa $321$
karyawan hanya menggunakan kereta dan ada sejumlah karyawan yang
menggunakan kedua alat transportasi tersebut. Jika dipilih satu karyawan
secara acak, berapakah peluang terpilihnya karyawan yang pergi bekerja
menggunakan bus atau kereta?
Diketahui $445$ karyawan menggunakan kereta dan $321$ karyawan yang
hanya menggunakan kereta. Artinya, sebanyak $445-321 = \color{red}{124}$
karyawan sisanya merupakan pengguna bus atau kereta. Karena jumlah
karyawan seluruhnya ada $\color{blue}{1108}$, maka peluang terpilihnya
seorang karyawan yang pergi bekerja menggunakan bus atau kereta
adalah
$P(A) = \dfrac{\color{red}{124}}{\color{blue}{1108}} =
\dfrac{31}{277}$.
Soal Nomor 10
Nico, Raden, dan Violin pergi ke restoran dan akan memesan sandwich.
Restoran menyediakan $10$ tipe sandwich berbeda. Jika masing-masing dari
mereka menyukai setiap tipe sandwich, berapakah peluang kejadian
setidaknya dua dari mereka memilih tipe sandwich yang berbeda?
Misalkan $(a, a, a)$ menyatakan bahwa Nico, Raden, dan Violin sama-sama
memilih menu sandwich tipe $a$.
Ada $10$ kemungkinan mereka bertiga memilih tipe sandwich yang sama,
yaitu $(1, 1, 1), (2, 2, 2)$, dan diteruskan sampai $(10, 10,
10).$
Banyak kemungkinan pemilihan $10$ tipe sandwich adalah
$10 \times 10 \times 10 = 1000.$
Dengan menggunakan konsep peluang komplemen, diperoleh
$\begin{aligned} P(A^C) & = \dfrac{1000-10}{1000} \\ & =
\dfrac{990}{1000} = \dfrac{99}{100} \end{aligned}$
Jadi, peluang kejadian setidaknya dua dari mereka memilih tipe sandwich
yang berbeda adalah $\boxed{\dfrac{99}{100}}$
Soal Nomor 11
Peluang seseorang mengendarai sepeda adalah $\dfrac12$. Peluang orang
tersebut menaiki bus adalah $\dfrac13$. Berapa peluang orang tersebut
tidak mengendarai sepeda maupun menaiki bus?
Peluang orang tersebut tidak mengendarai sepeda maupun menaiki bus sama
dengan komplemen dari peluang orang itu mengendarai sepeda atau menaiki
bus, yaitu
$\begin{aligned} p(A^c \cup B^c) & = 1-P(A \cup B) \\ & =
1-\left(\dfrac12 + \dfrac13\right) \\ & = 1-\dfrac56 = \dfrac16
\end{aligned}$
Soal Nomor 12
Dua buah dadu dilambungkan secara bersamaan. Frekuensi harapan dari
kejadian jumlah mata dadu kurang dari $9$ adalah $65$. Berapa kali dadu
itu dilambungkan?
Banyak titik sampel untuk jumlah mata dadu $2$ adalah $1$, yaitu $(1,
1)$.
Banyak titik sampel untuk jumlah mata dadu $3$ adalah $2$, yaitu $(1,
2), (2, 1)$.
Jika diteruskan, kita akan menemukan pola bahwa banyak titik sampelnya
selalu bertambah $1$ sampai jumlah mata dadu $7$, lalu menurun $1$ untuk
mata dadu $8$ sampai $12$.
Titik sampel dari pelambungan dua dadu dengan jumlah mata dadu kurang
dari $9$ ada sebanyak $1+2+3+4+5+6+5 = \color{blue}{26}$.
Banyak titik sampel seluruhnya:
$6 \times 6 = \color{red}{36}$.
Misalkan dadu dilambungkan sebanyak $n$ kali. Karena frekuensi harapan
dari kejadian jumlah mata dadu kurang dari $9$ adalah $65$, maka kita
tuliskan
$\begin{aligned}
\dfrac{\cancelto{13}{\color{blue}{26}}}{\cancelto{18}{\color{red}{36}}}
\times n & = 65 \\ n & = \cancelto{5}{65} \times
\dfrac{18}{\cancel{13}} \\ & = 5 \times 18 = 90 \end{aligned}$
Jadi, dadu tersebut dilambungkan sebanyak $90$ kali.
Soal Nomor 13
Anggaplah kamu memiliki satu stoples kacang. Kamu mengambil $100$ butir
kacang secara acak dan memberi tanda titik merah pada setiap kacang
sebelum memasukannya kembali ke dalam stoples. Lalu kamu mengambil $100$
butir kacang lagi secara acak dan $20$ di antaranya memiliki titik merah.
Dalam kondisi ideal, berapa banyak butir kacang yang ada di dalam
stoples?
Dengan menandai $100$ butir kacang dan hanya menemukan $20$ dari $100$
butir kacang bertitik merah, maka itu artinya kamu menemukan $1$ kacang
bertitik merah dari setiap $5$ butir kacang yang diambil. Jika $100$
kacang bertitik merah adalah sampel, maka akan ada $\boxed{5 \times 100
= 500}$ butir kacang di dalam stoples tersebut (dalam kondisi ideal).
🎯Terimakasih, anda telah membaca postingan dengan judul:
📚 "Materi SMP Tentang Peluang (Probabilitas) SMP |Soal-Soal dan Pembahasan|", semoga postingan ini bermanfaat untuk anda."Matematika adalah bahasa yang digunakan alam untuk berbicara dengan kita." 😊- Galileo Galilei
 SMP |Soal-Soal dan Pembahasan|){kind=link}