Dasar-dasar Fungsi Linier-SMP
📊 Pengantar Fungsi Linier & Kuadrat beserta Contoh dan Latihan Interaktif
✨ Fungsi Linier dalam Matematika SMP
Fungsi linier adalah fungsi yang menghasilkan grafik berupa garis lurus dengan bentuk umum:
$\boxed{f(x) = mx + c}$
Di mana m adalah kemiringan garis (gradien) dan c adalah titik potong garis dengan sumbu y. Fungsi ini menggambarkan hubungan yang berubah dengan laju konstan.
🔶 Perbedaan Fungsi Linier dan Fungsi Kuadrat
| Aspek | Fungsi Linier | Fungsi Kuadrat |
|---|---|---|
| Bentuk Persamaan | $f(x) = mx + c$ | $f(x) = ax^{2} + bx + c$ |
| Grafik | Garis lurus | Kurva parabola |
| Variabel Pangkat | Satu (linear) | Dua (kuadrat) |
| Gradien | Konstan | Tidak konstan, melengkung |
| Titik Potong Sumbu X | Maksimal satu | 0, 1, atau 2 titik |
| Bentuk Kurva | Linear lurus | Parabola buka atas atau bawah |
📐 Cara Menggambar Grafik Fungsi Kuadrat
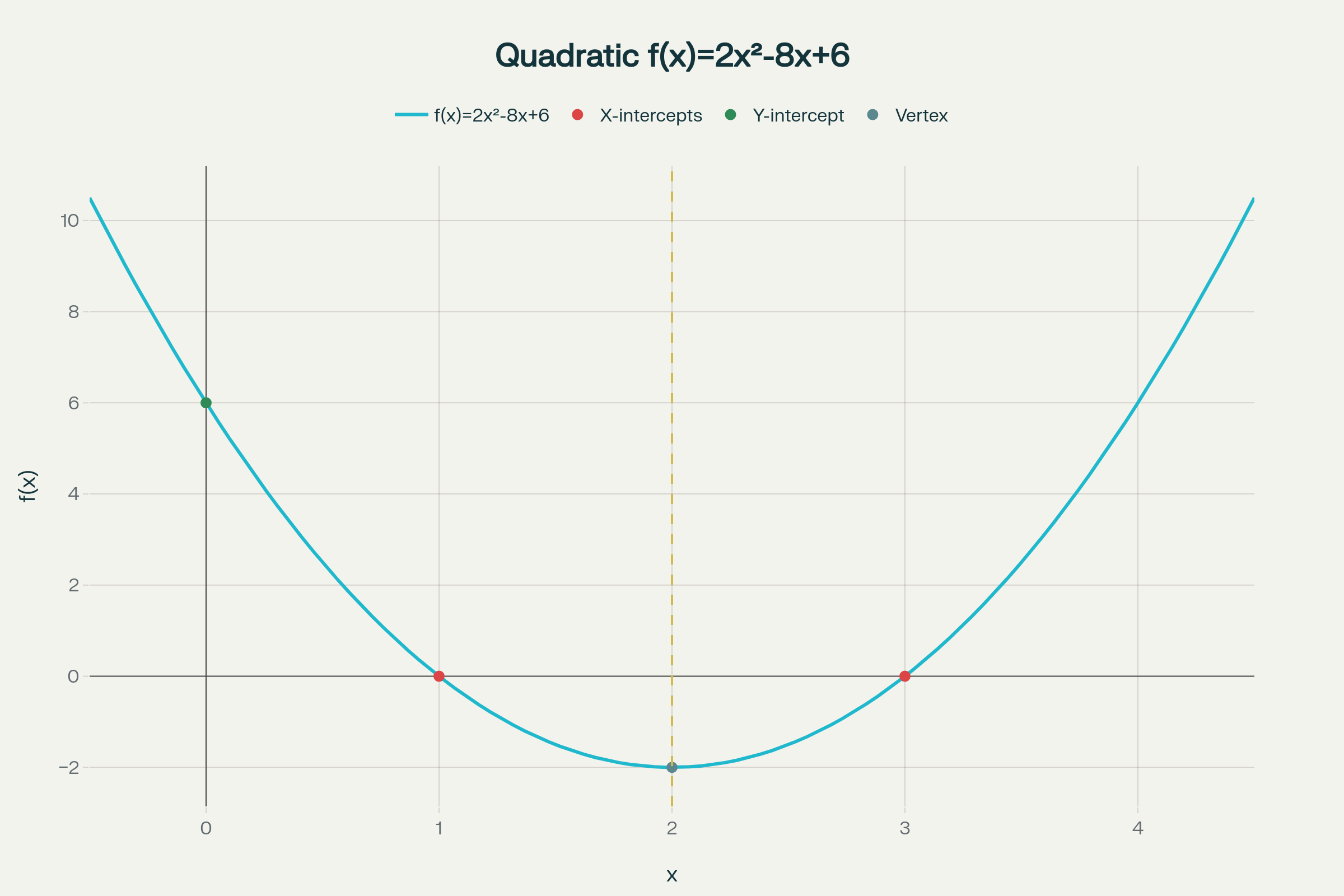
Misal kita memiliki fungsi $f(x) = 2x^{2} - 8x + 6$. Langkah menggambar:
- Tentukan arah parabola. Karena \(a = 2 > 0\), parabola terbuka ke atas.
- Titik potong sumbu $x$ dengan menyelesaikan persamaan kuadrat, didapat titik potong $(1,0)$ dan $(3,0)$.
- Titik potong sumbu $y$ adalah $(0,6)$.
- Hitung sumbu simetri dengan rumus $x = -\dfrac{b}{2a}= 2$.
- Hitung titik puncak dengan substitusi: $f(2) = -2$, jadi titik puncak $(2,-2)$.
- Gambar parabola yang simetris terhadap garis vertical $x=2$ dan melalui titik-titik penting tersebut.
⚡ Cara Cepat Menentukan Titik Puncak dan Sumbu Simetri
Gunakan rumus ini untuk fungsi kuadrat \( f(x) = ax^2 + bx + c \):
- Sumbu simetri: \( x = -\dfrac{b}{2a} \)
- Titik puncak: \( \left(-\dfrac{b}{2a}, f\left(-\dfrac{b}{2a}\right)\right) \)
🔥 Contoh Cepat Hitung Titik Puncak
Pada fungsi \( f(x) = 2x^2 - 8x + 3 \):
- Sumbu simetri: \( x = 2 \)
- Titik puncak:
\( y = f(2) = 2(2)^2 - 8(2) + 3 = -5 \) Jadi, titik puncak adalahd $(2, -5)$.
📝 Latihan Interaktif Fungsi Linier
Isi jawaban dan klik tombol untuk cek jawabanmu!
🎯Terimakasih, anda telah membaca postingan dengan judul:
📚 "Dasar-dasar Fungsi Linier-SMP", semoga postingan ini bermanfaat untuk anda."Matematika adalah bahasa yang digunakan alam untuk berbicara dengan kita." 😊- Galileo Galilei