Teorema Pythagoras dan Aplikasinya - Materi Olimpiade

Teorema Pythagoras dan Aplikasinya
Materi Olimpiade Matematika
Teorema Pythagoras dan Aplikasinya
Untuk segitiga siku-siku dengan dua sisi siku-siku \(a, b\) dan sisi miring \(c\), jumlah kuadrat sisi siku-siku sama dengan kuadrat sisi miring, yaitu \(a^2 + b^2 = c^2\).
Jika panjang \(a, b, c\) dari tiga sisi segitiga memiliki hubungan \(a^2 + b^2 = c^2\), maka segitiga tersebut harus merupakan segitiga siku-siku dengan sisi siku-siku \(a, b\) dan sisi miring \(c\).
Ketika menyelidiki segitiga siku-siku, kesimpulan berikut sering digunakan:
Sebuah segitiga adalah segitiga siku-siku, jika dan hanya jika median pada satu sisi adalah setengah dari sisi tersebut.
Jika segitiga siku-siku memiliki sudut interior berukuran \(30^\circ\), maka sisi yang berlawanan dengan sudut tersebut adalah setengah dari sisi miring.
Contoh
Diketahui keliling segitiga siku-siku adalah \((2 + \sqrt{6})\) cm, median pada sisi miring adalah 1 cm. Temukan luas segitiga.
Teorema III menyiratkan bahwa \(AD = BD = CD = 1\), sehingga \(AB = 2\). Misalkan \(AC = b, BC = a\), maka
\[ a^2 + b^2 = 2^2 = 4 \quad \text{dan} \quad a + b = \sqrt{6}. \]
Oleh karena itu \( 6 = (a + b)^2 = a^2 + b^2 + 2ab \), sehingga
\[ ab = \frac{6 - 4}{2} = 1, \]
luas segitiga \( ABC \) adalah \(\frac{1}{2}\).
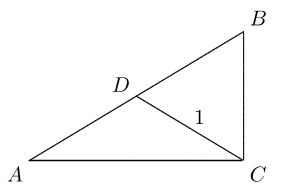
Seperti yang ditunjukkan pada gambar, \( \angle C = 90^\circ, \angle 1 = \angle 2, CD = 1.5 \, \text{cm}, BD = 2.5 \, \text{cm}. \) Temukan \( AC \).
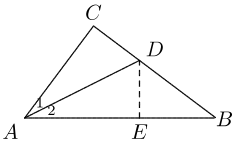
Dari \( D \) buat \( DE \perp AB \), memotong \( AB \) di \( E \). Ketika kita melipat bidang yang memuat \( \triangle CAD \) sepanjang garis \( AD \), maka \( C \) bertepatan dengan \( E \), sehingga
\[ AC = AE, \quad DE = CD = 1.5 \, (\text{cm}). \]
Dengan menerapkan Teorema Pythagoras pada \( \triangle BED \),
\[ BE = \sqrt{BD^2 - DE^2} = \sqrt{6.25 - 2.25} = 2 \, (\text{cm}). \]
Misalkan \( AC = AE = x \) cm dan menerapkan Teorema Pythagoras pada \( \triangle ABC \) menghasilkan persamaan
\[ \begin{cases} (x + 2)^2 = x^2 + 4^2, \\ 4x = 12, \quad x = 3. \end{cases} \]
Jadi \( AC = 3 \, \text{cm} \).
Seperti yang ditunjukkan pada gambar, \( ABCD \) adalah persegi, \( P \) adalah titik interior sehingga \( PA : PB : PC = 1 : 2 : 3 \). Temukan \( \angle APB \) dalam derajat.
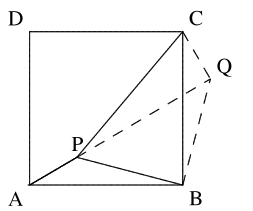
Tanpa mengurangi keumuman, kita asumsikan bahwa \( PA = 1, PB = 2, PC = 3 \). Putar \( \triangle APB \) di sekitar \( B \) sebesar \( 90^\circ \) searah jarum jam, sehingga \( P \rightarrow Q, A \rightarrow C \), maka \( \triangle BPQ \) adalah segitiga siku-siku sama kaki, oleh karena itu
\[ PQ^2 = 2PB^2 = 8, CQ^2 = PA^2 = 1, \]
oleh karena itu, dengan Teorema Pythagoras,
\[ PC^2 = 9 = CQ^2 + PQ^2, \quad \angle CQP = 90^\circ. \]
Jadi \( \angle APB = \angle CQB = 90^\circ + 45^\circ = 135^\circ \).
Diagram menunjukkan segi enam \( ABCDEF \) yang terdiri dari lima segitiga siku-siku sama kaki \( ABO, BCO, CDO, DEO, EFO \), dan segitiga \( AOF \), di mana \( O \) adalah titik perpotongan garis \( BF \) dan \( AE \). Diketahui \( OA = 8 \, \text{cm} \), temukan luas \( \triangle AOF \) dalam \( \text{cm}^2 \).
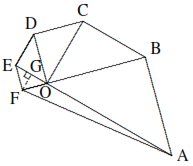
Dari
\[OC = \frac{1}{\sqrt{2}}OB = (\frac{1}{\sqrt{2}})^2OA = \frac{1}{2}OA,\]
\[OE = \frac{1}{\sqrt{2}}OC = \frac{1}{4}OA = 2 \, (\text{cm}).\]
Karena \( \text{Rt} \triangle EFO \sim \text{Rt} \triangle ABO \),
\[EF = OF = \frac{1}{4}OB = \frac{1}{4\sqrt{2}}OA.\]
Misalkan \( FG \perp AE \) di \( G \), maka \( FG = \frac{1}{\sqrt{2}}OF = \frac{1}{8}OA = 1 \, \text{cm} \). Jadi, luas \( \triangle AOF \), \( S_{\triangle AOF} \), diberikan oleh
\[S_{\triangle AOF} = \frac{1}{2}AO \cdot FG = 4 \, (\text{cm}^2).\]
Dalam \( \triangle ABC \), \( AM \) adalah median pada sisi \( BC \). Buktikan bahwa \( AB^2 + AC^2 = 2(AM^2 + BM^2) \).
Misalkan \( AD \perp BC \) di \( D \). Dengan Teorema Pythagoras,
\[AB^2 = BD^2 + AD^2 = (BM + MD)^2 + AD^2\]
\[= BM^2 + 2BM \cdot MD + MD^2 + AM^2 - MD^2\]
\[= BM^2 + AM^2 + 2BM \cdot MD.\]
Demikian pula, kita memiliki
\[AC^2 = CM^2 + AM^2 - 2MC \cdot MD.\]
Jadi, dengan menambahkan kedua persamaan, karena \( BM = CM \),
\[AB^2 + AC^2 = 2(AM^2 + BM^2).\]

Catatan: Ketika \( AM \) diperpanjang ke \( E \) sehingga \( ABEC \) adalah jajar genjang, maka rumus median sama dengan aturan jajar genjang:
\[AB^2 + BE^2 + EC^2 + CA^2 = AE^2 + BC^2.\]
Pada gambar, \( \angle C = 90^\circ \), \( \angle A = 30^\circ \), \( D \) adalah titik tengah \( AB \) dan \( DE \perp AB \), \( AE = 4 \, \text{cm} \). Temukan \( BC \).
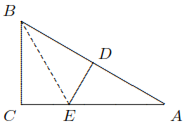
Hubungkan \( BE \). Karena \( ED \) adalah garis bagi tegak lurus \( AB \), \( BE = AE \), sehingga \( \angle EBD = \angle EBA = \angle A = 30^\circ \), \( \angle CBE = 60^\circ - 30^\circ = 30^\circ \), ∴ \( CE = \frac{1}{2} BE = DE = \frac{1}{2} AE = 2 \, \text{cm} \). Sekarang misalkan \( BC = x \, \text{cm} \), maka dari Teorema Pythagoras,
\[ (2x)^2 = x^2 + 6^2 \implies x^2 = 12 \implies x = \sqrt{12} = 2\sqrt{3} \, \text{cm}. \]
Jadi, \( BC = 2\sqrt{3} \, \text{cm} \).
Untuk \( \triangle ABC \), \( O \) adalah titik interior, dan \( D, E, F \) berada pada \( BC, CA, AB \) masing-masing, sehingga \( OD \perp BC, OE \perp CA \), dan \( OF \perp AB \). Buktikan bahwa \( AF^2 + BD^2 + CE^2 = BF^2 + DC^2 + AE^2 \).
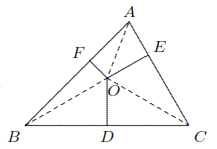
Dengan menerapkan Teorema Pythagoras pada segitiga \( OAF, OBF, OBD, OCD, OCE \) dan \( OAE \), maka
\begin{aligned} &AF^2 + BD^2 + CE^2 \\ &= AO^2 - OF^2 + BO^2 - OD^2 + CO^2 - OE^2 \\ &= (BO^2 - OF^2) + (CO^2 - OD^2) + (AO^2 - OE^2) \\ &= BF^2 + DC^2 + AE^2. \end{aligned}
Kesimpulan terbukti.
Pada diagram di bawah, \( P \) adalah titik interior \( \triangle ABC \), \( PP_1 \perp AB \), \( PP_2 \perp BC \), \( PP_3 \perp AC \), dan \( BP_1 = BP_2 \), \( CP_2 = CP_3 \), buktikan bahwa \( AP_1 = AP_3 \).
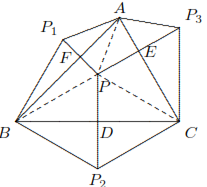
Untuk segi empat \( AP_1BP \), karena kedua diagonalnya saling tegak lurus,
\[ AP_1^2 + BP^2 = AF^2 + P_1F^2 + BF^2 + PF^2 = AP^2 + BP_1^2. \]
Dengan mempertimbangkan \( AP_3CP \) dan \( PCP_2B \) masing-masing, maka secara serupa diperoleh
\[ AP^2 + CP_3^2 = AP_3^2 + PC^2, \]
\[ BP_2^2 + PC^2 = PB^2 + CP_2^2. \]
Kemudian menjumlahkan ketiga persamaan menghasilkan
\[ AP_1^2 = AP_3^2, \therefore AP_1 = AP_3. \]
Dalam persegi \(ABCD\), \(M\) adalah titik tengah \(AD\) dan \(N\) adalah titik tengah \(MD\). Buktikan bahwa \(\angle NBC = 2\angle ABM\).
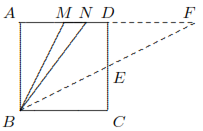
Misalkan \(AB = BC = CD = DA = a\). Misalkan \(E\) adalah titik tengah \(CD\). Misalkan garis \(AD\) dan \(BE\) berpotongan di \(F\).
Dengan simetri, kita memiliki \(DF = CB = a\). Karena segitiga siku-siku \(ABM\) dan \(CBE\) simetris dalam garis \(BD\), \(\angle ABM = \angle CBE\).
Cukup untuk menunjukkan \(\angle NBE = \angle EBC\), dan untuk ini kita hanya perlu menunjukkan \(\angle NBF = \angle BFN\) karena \(\angle DFE = \angle EBC\).
Dengan asumsi kita memiliki
\[AN = \frac{3}{4}a, \therefore NB = \sqrt{(\frac{3}{4}a)^2 + a^2} = \frac{5}{4}a.\]
Di sisi lain,
\[NF = \frac{1}{4}a + a = \frac{5}{4}a,\]
jadi \(NF = BN\), maka \(\angle NBF = \angle BFN\).
Soal Latihan (A)
Dalam \(\triangle ABC\), \(\angle A = 90^\circ\), \(AB = AC\), \(D\) adalah titik pada \(BC\). Buktikan bahwa \(BD^2 + CD^2 = 2AD^2\).
Diketahui bahwa \(\text{Rt}\triangle ABC\) memiliki keliling 30 cm dan luas 30 cm\(^2\). Temukan panjang ketiga sisinya.
Dalam \(\text{Rt}\triangle ABC\), \(\angle C = 90^\circ\), \(AD\) adalah garis bagi \(\angle A\) yang memotong \(BC\) di \(D\). Diketahui \(AB = 15\) cm, \(AC = 9\) cm, \(BD : DC = 5 : 3\). Temukan jarak \(D\) dari \(AB\).
Dalam segitiga siku-siku \(ABC\), \(\angle C = 90^\circ\), \(BC = 12\) cm, \(AC = 6\) cm, garis bagi tegak lurus \(AB\) memotong \(AB\) dan \(BC\) di \(D\) dan \(E\) masing-masing. Temukan \(CE\).
Dalam persegi panjang \(ABCD\), \(CE \perp DB\) di \(E\), \(BE = \frac{1}{4}BD\) dan \(CE = 5\) cm. Temukan panjang \(AC\).
Dalam \(\triangle ABC, \angle C = 90^\circ\), \(D\) adalah titik tengah \(AC\). Buktikan bahwa \[AB^2 + 3BC^2 = 4BD^2.\]
Dalam segitiga siku-siku \(ABC, \angle C = 90^\circ\), \(E, D\) adalah titik pada \(AC\) dan \(BC\) masing-masing. Buktikan bahwa \[AD^2 + BE^2 = AB^2 + DE^2.\]
\(\triangle ABC\) adalah segitiga sama kaki dengan \(AB = AC = 2\). Ada 100 titik \(P_1, P_2, \ldots, P_{100}\) pada sisi \(BC\). Tulis \(m_i = AP_i^2 + BP_i \cdot P_iC (i = 1, 2, \ldots, 100)\), temukan nilai dari \(m_1 + m_2 + \cdots + m_{100}\).
Dalam \(\triangle ABC, \angle C = 90^\circ\), \(D\) adalah titik tengah \(AB, E, F\) adalah dua titik pada \(AC\) dan \(BC\) masing-masing, dan \(DE \perp DF\). Buktikan bahwa \(EF^2 = AE^2 + BF^2\).
Diketahui bahwa \(P\) adalah titik interior segitiga sama sisi \(ABC\), sehingga \(PA = 2, PB = 2\sqrt{3}, PC = 4\). Temukan panjang sisi \(\triangle ABC\).
Soal Latihan (B)
\(AB\) adalah tali busur dalam lingkaran dengan pusat \(O\) dan jari-jari 52 cm. Titik \(M\) membagi tali busur \(AB\) sehingga \(AM = 63\) cm dan \(MB = 33\) cm. Temukan panjang \(OM\) dalam cm.
\(ABCD\) adalah persegi panjang, \(P\) adalah titik interior persegi panjang sehingga \(PA = 3, PB = 4, PC = 5\), temukan \(PD\).
Tentukan apakah ada segitiga siku-siku seperti itu: setiap sisinya adalah bilangan bulat dan satu sisi siku-siku adalah kelipatan dari sisi siku-siku lainnya.
Dalam persegi panjang \(ABCD, \angle C\) dibagi tiga oleh \(CF\) dan \(CE\), di mana \(E\) berada pada \(AB, F\) berada pada \(AD, BE = 6\) dan \(AF = 2\). Manakah dari berikut ini yang paling mendekati luas persegi panjang \(ABCD\)? (A) 110, (B) 120, (C) 130, (D) 140, (E) 150.
Misalkan \(ABCD\) adalah segi empat cembung. Buktikan bahwa \(AC \perp BD\) jika dan hanya jika \(AB^2 + CD^2 = AD^2 + BC^2\).
🎯Terimakasih, anda telah membaca postingan dengan judul:
📚 "Teorema Pythagoras dan Aplikasinya - Materi Olimpiade", semoga postingan ini bermanfaat untuk anda."Matematika adalah bahasa yang digunakan alam untuk berbicara dengan kita." 😊- Galileo Galilei